Свойства дифференциала функции
Задача нахождения дифференциала функции сводится к нахождению производной функции , так как 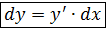 , поэтому все свойства производной распространяются и на дифференциал:
, поэтому все свойства производной распространяются и на дифференциал:
1). d(u 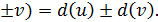
2). d(u 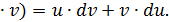
3). d( 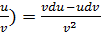 .
.
Пример 1.Найти дифференциал функции y = 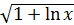 .
.
Решение.dy = 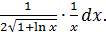
Пример 2. Найти дифференциал функции y, если sin(x+y) = 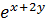 .
.
Решение.Функция y задана неявно , найдём сначала y’ . Дифференцируем обе части равенства cos(x+y)(1+y’) = 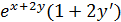 отсюда выражаем y’ .
отсюда выражаем y’ .
Y’ = 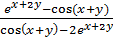 =
= 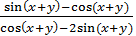 , dy =
, dy = 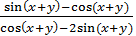 dx.
dx.
Инвариантность формы дифференциала функции
Если y = f(u) , где u = 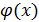 , y = f[
, y = f[ 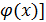 , то
, то 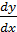 = f’u (u)
= f’u (u) 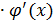 → dy = f’u
→ dy = f’u 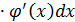
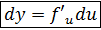 .
.
du
Вывод.Форма дифференциала не зависит от того , является аргумент функции независимой переменной или функцией другого аргумента.
Пример.Найти дифференциал функции y = sin 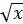 .
.
Решение.y = sinu , u = 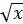 , dy = cosu
, dy = cosu 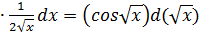 .
.
Геометрическое значение дифференциала функции
y
M1
T 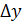
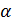
M N
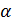 x
x
0 x x+ 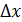
М(x,y) ; M 1(x+ 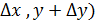 ; NT = MN
; NT = MN 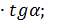 tg
tg 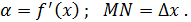
NT = f’(x) 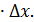 →
→ 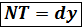
Вывод. Дифференциал функции f(x) , соответствующий значениям x и 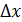 равен приращению ординаты касательной к кривой y = f(x) в данной точке x.
равен приращению ординаты касательной к кривой y = f(x) в данной точке x.
Замечание. В данном случае 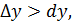 но возможно и
но возможно и 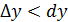 .
.
y N
M2 Т 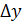
М1
0 x NT = dy 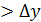
Дата добавления: 2016-06-05; просмотров: 2336;











