Непрерывность функции
Пусть функция y= f(x) определена при некотором значении x0 и y0 = f(x0 ). Если x получит приращение 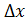 , то и функция y получит приращение
, то и функция y получит приращение 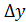 , то есть f(x0 +
, то есть f(x0 + 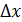 ) = y0 +
) = y0 + 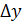

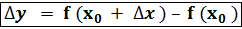
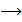 приращение функции.
приращение функции.
Определение 1. Функция y= f(x) называется непрерывнойв точке x = x0 , если она определена в этой точке и если  , то есть бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
, то есть бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Пример. Показать , что функция y = 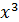 непрерывна в произвольной точке.
непрерывна в произвольной точке.
Решение.Область определения этой функции вся числовая ось.Составим приращение функции 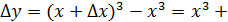
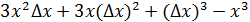 , перейдём к пределу
, перейдём к пределу 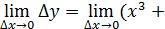
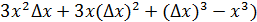 =0
=0
Вывод.Функция y = 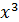 непрерывна всюду.
непрерывна всюду.
Определение 2. Пусть функция y= f(x) непрерывна в точке x0 , тогда 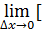 f(x0 +
f(x0 + 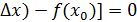 или
или 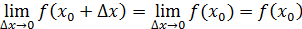
В последнем равенстве обозначим x0 + 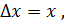 при
при 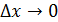 x
x 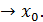
 . Окончательно, функция f(x) называется непрерывной в точке x0 , если
. Окончательно, функция f(x) называется непрерывной в точке x0 , если
1. f(x) – определена в точке x0 и в некоторой её окрестности.
2. f(x) имеет предел при x = x0 , это значит , что она имеет предел слева , справа и они равны между собой , и равны значению функции в точке x =x0 .

Если в какой либо точке x0 одно из условий не выполняется , функция называется разрывной в этой точке , точка x0 называется точкой разрыва.
Определение.
1. Точкой разрыва 1-го рода функции y=f(x) называется такая точка x0 в кото-
рой функция имеет левый и правый пределы неравные между собой.
2. Точкой разрыва 2-го рода или бесконечного разрываназывается точка x0 в которой хотя бы один из пределов не существует или равен 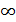 .
.
Пример 1.Установить характер точки разрыва функции y =  .
.
Решение.В точке x=0 функция не существует , то есть 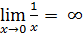 ,значит x=0 точка разрыва 2-го рода. Чтобы изобразить график функции в окрестности точ-
,значит x=0 точка разрыва 2-го рода. Чтобы изобразить график функции в окрестности точ-
ки разрыва , найдём пределы слева и справа.
y
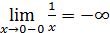 ;
; 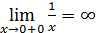 .
.
x
Пример 2.Установить характер точек разрыва для функции y= 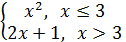
Решение.В окрестности точки x=3 функция меняет своё значение , поэтому в этой точке может быть разрыв . Проверим это , найдём все пределы.
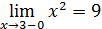 ;
; 
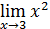 =9; y(3)=9.
=9; y(3)=9.
Ответ.Так как предел слева не равен пределу справа , то x=3 точка разрыва 1-го рода. y
9- - - - - -
7-- - - - -
0 3 x
Теорема 1.Если функции 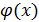 и
и 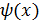 непрерывны в точке x0 , то их сумма , произведение, отношение также непрерывны в точке x0 , при
непрерывны в точке x0 , то их сумма , произведение, отношение также непрерывны в точке x0 , при 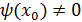 , то есть
, то есть 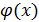
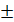
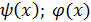

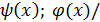
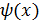 - непрерывные функции.
- непрерывные функции.
Теорема 2.Сложная функция y = f [ 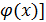 , образованная из 2-х непрерывных функций f (x) и
, образованная из 2-х непрерывных функций f (x) и 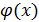 есть функция непрерывная.
есть функция непрерывная.
Пример.Y = sin (x3 + 4x – 2) ; y = 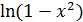
 .
.
Дата добавления: 2016-06-05; просмотров: 2127;











