Поверхности вращения

Определение.Поверхность , образованная вращением линии около оси , называется поверхностью вращения.

Пусть линия L , лежащая в плоскости оxz , задана уравнением

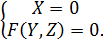(1)

Получим уравнение поверхности , образованной вращением этой линии относительно оси оz

z N(0,Y,Z) ; M (x,y,z) - точка поверх-

ности. К – точка пересечения плоскости ,

L ⊥-ой оси вращения, N – точка пе -

K

.N ресечения плоскости ⊥-ой оси оz.

M

x 0 y

KN и KM – радиусы окружности , КN=KM. Длина KN = 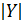, KM=OP= 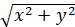и 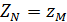, так как точка N лежит на линии L (1) , то координаты точки N ( O,Y,Z) удовлетворяют второму уравнению из (1) , подставим в него F ( 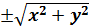, z )=0 . → Уравнение поверхности вращения вокруг оси oz. Аналогично , вокруг оси ox F ( 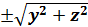, x )=0 ,вокруг оси oy F ( 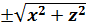, y )=0 .

Пример 1. Записать уравнение поверхности вращения линии 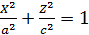вокруг оси oz.

Решение.В данном уравнении заменим 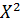на 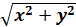получим 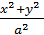+ 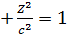это эллипсоид вращения.

Пример 2. Записать уравнение поверхности , полученной от вращения линии 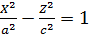вокруг оси ox.

Решение. В данном уравнении 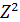заменим на 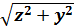,получим 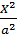- 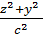=1

это двуполостный гиперболоид.

Лекция 15. Преобразование прямоугольной системы координат в . Квадратичные формы.