Адсорбция на однородной поверхности
2.4.2.1.Уравнение Ленгмюра(*)
Различают адсорбцию газа на твердом теле, адсорбцию растворенного вещества на границе раствор/газ, адсорбцию растворенного вещества на границе твердое тело/раствор.
Адсорбция газа на твердом теле является простейшим случаем адсорбции, т.к. эта система состоит из двух компонентов. Поэтому адсорбция газа твердым телом удобна для теоретического рассмотрения явления адсорбции.
Имеется несколько теорий физической адсорбции, из которых рассмотрим прежде всего теорию мономолекулярной адсорбции. Эта теория была предложена в 1915 г. американским ученым Ленгмюром, при разработке которой были использованы представления об адсорбционных силах, впервые выдвинутые русским ученым Л.Г.Гурвичем(*). При разработке теории Ленгмюр исходил из следующих положений.
Основные положения теории Ленгмюра:
1. Адсорбция мономолекулярная
2. Адсорбция локализована, т.е. на поверхности адсорбента существуют центры адсорбции
3. Адсорбция идет на энергетически однородной поверхности, т.е. центры адсорбции обладают одинаковой избыточной энергией, и адсорбированные молекулы не взаимодействуют друг с другом
Таким образом, на поверхности адсорбента находятся одинаковые центры адсорбции, каждый из которых может адсорбировать только одну частицу.
Рассмотрим динамическое равновесие между молекулами в газовой фазе и адсорбированными на поверхности как квазихимическую реакцию:
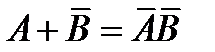
А – молекулы газовой фазы, В – центры адсорбции на поверхности адсорбента.
При равновесии: vадс = vдес
Vадс= kадс Р (1-Θ), (2.38)
где Θ – доля занятой поверхности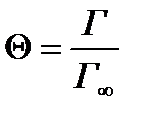 
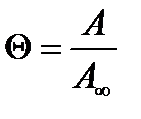, (А∞ и Г∞ - максимально возможная адсорбция на всех центрах адсорбции единицы поверхности).
Vдес= kдес Р Θ (2.39)
При равновесии:
kадс Р (1-Θ) = kдес Р Θ (2.40)
отсюда:
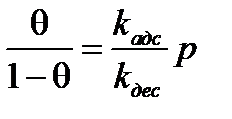, т.е. 
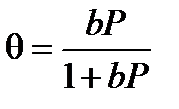(2.41)
где b – адсорбционный коэффициент, равный отношению констант адсорбции и десорбции.
Уравнения Ленгмюра можно записать в виде:
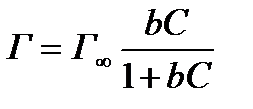
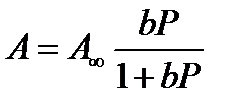
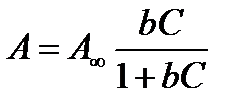(2.42)
Графически изотерма Ленгмюра представлена на рис.2.15:
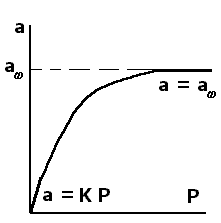
Рис 2.15 Изотерма мономолекулярной адсорбции
При Р→0 уравнение Ленгмюра переходит в уравнение Генри(*):
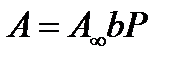=КГ Р (2.43)
В этом случае мы имеем линейную зависимость между А и Р, её часто называют изотермой Генри, при этом КГ называют константой Генри, а область малых Р – областью Генри. На рис. 2.15 область Генри представлена прямой линией, выходящей из начала координат.
Если b×P >> 1 (область высоких давлений), то уравнение Ленгмюра преобразуется к виду:
А = А¥ (2.44)
В этом случае наблюдается независимость А от Р: при больших Р все центры адсорбции заполнены (на каждой «клетке доски» уже стоит своя «фигура») и дальнейшее увеличение давления не изменяет адсорбции. На рис. 2.15 эта область изображена прямой, параллельной оси абсцисс. Между двумя указанными областями мы имеем кривую – гиперболу.
Наклон кривой определяется константой равновесия b, которая в свою очередь зависит от энергии взаимодействия адсорбата и адсорбента и зависит от температуры: с увеличением температуры b экспоненциально уменьшается.
Покажем это.
Первый вариант:
Уравнение Аррениуса учитывает влияние температуры на константу скорости химической реакции: 
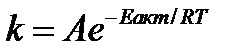(2.45)
lnk
tgα = -E/RT, где α — угол наклона прямой (2.46)
1/T
Так как b – это отношение констант скоростей процессов, то можно записать:
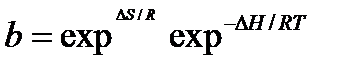, (2.47)
т.к. Еакт может быть представлена соотношением: Еакт= ΔН – ТΔS (2.48)
Соотношение констант адсорбции и десорбции с увеличением температуры уменьшается, причем по экспоненте, т.к. ΔНадс всегда <0. Поэтому адсорбция с увеличением температуры количественно всегда уменьшается.
Или так:
Адсорбционный коэффициент b характеризует способность веществ адсорбироваться на поверхности, т.е. степень его «сродства» к адсорбционным центрам адсорбента. На рис. 2.16.а представлены изотермы адсорбции при различных значениях b3 > b2 > b1. Как и всякая константа равновесия, адсорбционный коэффициент связан с теплотой адсорбции DHa уравнением изотермы Вант-Гоффа(*) (2.47):
.
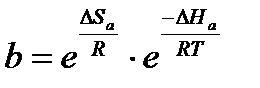Так как всегда DHa < 0, то с повышением температуры b экспоненциально уменьшается, т.е. и физическая, и химическая адсорбции (величины А или Г) уменьшаются с повышением температуры (см. изобару адсорбции на рис.2.12).
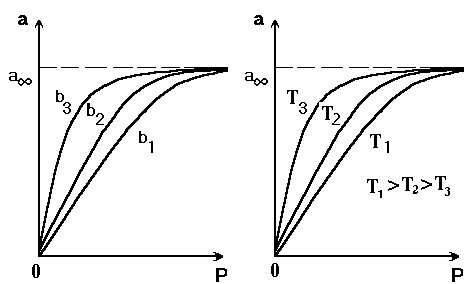
a b
Рис.2.16. Изотермы Ленгмюра при различных значениях константы b: b3>b2>b1 (а), и температуры Т: Т1>T2>T3 (b).
Изостера адсорбции на рис.2.12 также иллюстрирует данное положение: при повышении температуры адсорбция снижается и для поддержания её постоянного значения (А или q = const) следует увеличивать давление. Следует, однако, помнить, что А¥ и Г¥ зависят только от количества адсорбционных центров и при всех температурах они одинаковы (рис.2.16.b). 
Дата добавления: 2016-07-27; просмотров: 3058;
Поиск по сайту
Узнать еще
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
Публикации по медицине
