Построение поверхностей по их уравнениям методом сечений

1. Такой метод продемонстрируем на эллипсоиде.

Определение.Поверхность , определяемая уравнением

(1)

называется эллипсоидом. Числа 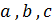называются полуосями эллипсоида.

Определим форму эллипсоида. Так как x , y , z в чётных степенях , то эллипсоид симметричен относительно осей ox , oy , oz. Пересечём его плоскостью z=h.

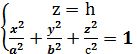
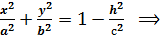
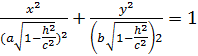
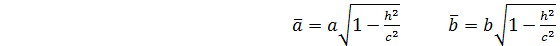(2)

0 y Из (2) видно , что с возрастанием h , полу-

оси эллипса и 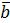уменьшаются. Можно показать , что при пересечении плоскостя-

x ми x = h и y = h , тоже будут эллипсы. Если

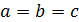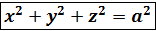, –cфера.

2. Гиперболоиды.

Каноническое уравнение гиперболоида имеет вид:

(1) - однополостный гиперболоид

Эта поверхность имеет три плоскости симметрии , так как x , y , z в чётных

степенях . Чтобы построить эту поверхность, надо её пересечь плоскостями параллельными координатным плоскостям. В (1) полагаем y=0 , в плоскости XOY

z получаем гиперболу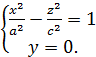

0 y В плоскости ZOY тоже гипербола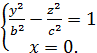

x В плоскости XOY – эллипс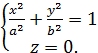

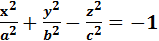- двуполостный гиперболоид , минус перед z ука- зывает на ось симметрии.

z

0 y

x

3. Параболоиды

Эллиптический параболоид 2z = 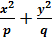-симметричный относительно оси оz.

z

0 y

x

Гиперболическийпараболоид (седло) 2z = 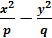, p>0 , q>0.

z

Y

x