Лекция14. Поверхности второго порядка

Определение. Поверхностью второго порядка называется множество точек пространства координаты x , y которых , удовлетворяют уравнению

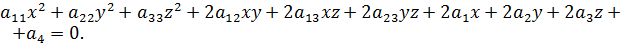(1)

. Сфера.

Если в уравнении (1) отсутствуют члены с произведением переменных , а коэффициенты при квадратах равны , то это всегда уравнение сферы , его можно привести к каноническому виду : (x - 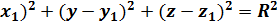, где

С ( 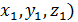- центр сферы , а R – радиус.

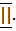Цилиндрическиеповерхности.

Определение.Поверхность , составленная из всех прямых , пересекающих данную линию L и параллельных данной прямой , называется цилиндрическойповерхностью. При этом линия L –направляющая , а линия - образующая.

Рассмотрим в плоскости OXY некоторую линию L , имеющую в системе координат уравнение

F ( x , y ) = 0 (2)

Покажем , что это уравнение цилиндрической поверхности.

z Точка N – проекция точки М на плоскость XOY,

точка N лежит на L и удовлетворяет уравнению

(2). Точки M и N имеют одну и ту же абсциссу и

.M(x,y,z) ординату , и удовлетворяют уравнению (2), так

0 y как оно не содержит z. Координаты другой точки

не удовлетворяют уравнению (2). Таким обра-

x .N L -зом координаты любой точки цилиндрической

поверхности удовлетворяют уравнению (2) , что

и хотели доказать.

Уравнение F(x, y)=0является уравнением цилиндрической поверхности с образующими параллельными оси OZ и направляющей L , которая в плоскости OXY задаётся тем же уравнением F (x , y )=0. Аналогично , можно показать , что уравнение F (x , z )= 0 – уравнение цилиндрической поверхности с образующими параллельными оси OY, F (y ,z ) = 0 –уравнение цилиндрической поверхности с образующими параллельными оси OX. 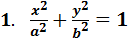- эллиптический цилиндр с образующими параллельными

z оси OZ , если 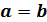, то круговой цилиндр.

0 y

2. - 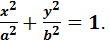– гиперболический3. 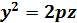– параболическийци-

цилиндр . –линдр , с образующими , парал-

лельными оси OX.

Z z

0 y 0 y

X x

. Коническиеповерхности.

Определение. Поверхность , составленная из всех прямых , пересекающих линию L и проходящих через данную точку Р , называется конической поверхностью. Линия L называется направляющей, точка Р - вершиной , а каждая из прямых , составляющих коническую поверхность – образующей .

Рассмотрим коническую поверхность с вершиной в начале координат и направляющей – эллипс.

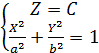(1) Это конус второго порядка.

Выберем произвольную точку М (x , y , z ) и проведём образующую ОМ , пересекающую направляющую в точке N ( X , Y , C ). Уравнение прямой ОМ , прохо-

z дящей через две точки О ( 0,0 ,0 ) и

L .N N ( X , Y , C ) имеет вид :

.M 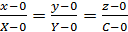или 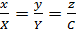отсюда

0 y X = 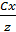, Y = 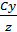эти значения подста-

x вим в (1).

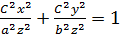
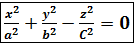→ Каноническое уравнение конуса 2-го порядка , симметричного относительно оси OZ.

Если 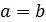, то 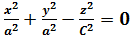→ прямой круговой конус.