МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Лекция 16. Понятие множества, функции, предела функции.
Понятие множества
Определение. Множество – это совокупность каких – либо объектов . Обозначаются множества А , В , М… . Элементы множества обозначаются a,b,c ,x ,y … .
Если элемент принадлежит множеству,то x Є M , если не принадлежит,то x 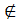 M.
M.
Определение. Объединениемили суммой множеств Мi называется множество М всех элементов , принадлежащих хотя бы одному из множеств Мi .
Обозначается: М = М1 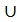 М2
М2 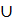 …
… 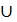 Мn или М =
Мn или М = 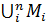
| М4 |
| М3 |
| М2 |
| М1 |
ММ
М = М1 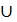 М2
М2 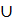 М3
М3 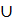 М4
М4
Определение. Пересечением множеств М1 , М2 …..Мn называется множество
М = М1 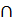 М2
М2 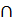 М3 …
М3 … 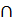 Мn , которому принадлежат элементы всех множеств Мn одновременно.
Мn , которому принадлежат элементы всех множеств Мn одновременно.
| М1 |
| М |
| М2 |
М = М1 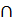 М2
М2
Символ 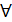 x означает ‘’ для всех x ‘’ или ‘’ для каждого x ‘’ или ‘’каково бы ни было x “,” для любого x “ . Символ
x означает ‘’ для всех x ‘’ или ‘’ для каждого x ‘’ или ‘’каково бы ни было x “,” для любого x “ . Символ 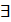 x читается “ существует такое x ,что “ или “ для некоторых x “. А
x читается “ существует такое x ,что “ или “ для некоторых x “. А  В из А следует В ; А
В из А следует В ; А 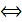 В из А следует В и наоборот из В следует А.
В из А следует В и наоборот из В следует А.
Понятие функции
Определение. Функциейназывается правило(соответствие) , по которому каждому элементу x некоторого множества М соответствует единственный элемент y другого множества L . Предполагаем , что М и L множества вещественных чисел.
| y |
| x |
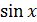 .
.
Sin
M L
Определение. Совокупность значений x , для которых определяются значения y в силу правила f(x) , называется областью определения функции или областью существования .
Определение.Множество всех значений , принимаемых функцией y называется областью значенийфункции.
Дата добавления: 2016-06-05; просмотров: 2045;











