Упрощение общего уравнения кривой второго порядка

Пример 1.С помощью параллельного переноса осей получить простейшее уравнение кривой и построить её: .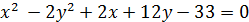

Решение.Выделим полные квадраты ( 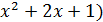- 1 – 2( 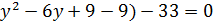; ( x+1 → –

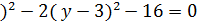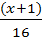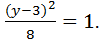
Положим 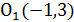; x = X-1; y = Y+3 → X= x + 1; Y = y – 3 ; получаем каноническое уравнение гиперболы в новых координатах :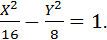

Y y

2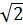

4 O₁ 4 X

2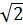

O x

Пример 2. Поворотом осей координат на 4 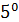упростить уравнение кривой и построить её 5 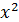- 6xy + 5 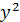= 32.

Решение.Запишем формулы поворота осей на 4 .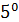

x = x’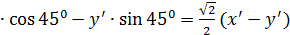

y = x’ , подставим эти значения x и y в уравнение кривой 5 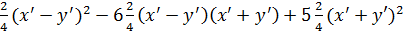=32 , произведя сокращения коэффициентов и раскрыв скобки , получим

x 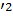+4y 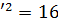или , разделив на 16, 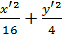= 1 , в новых координатах строим эллипс. Y x’

y’

2 4

o 45⁰ x

4

Квадратичные формы

Определение.Квадратичной формой Q ( x ) в n-мерном пространстве называется скалярное произведение следующего вида : Q ( 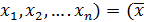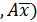, если 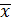= ( 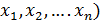,если же 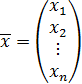, то ( =

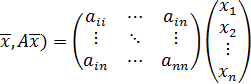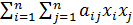= , то есть Q (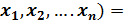 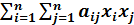,где .

Определение.Квадратичная матрица называется симметричной , если она не меняется при транспонировании , то есть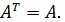

Пусть n=3 , A = 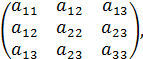если n=2 , то Q ( .

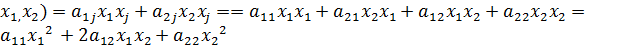Определение.Канонической квадратичной формой называется квадратичная форма , содержащая только квадраты переменных.

Если n = 2 , то Q ( 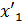, , 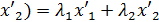где 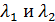собственные числа матрицы А = 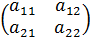. С помощью квадратичных форм можно кривые второго порядка приводить к каноническому виду , а также определять тип кривой.

Определение.Кривые второго порядка : эллипс , гипербола , парабола задаются квадратичными формами в двумерном пространстве , причём , если :

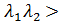
1). 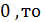- эллипс.

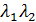
2). , то – гипербола .

3). 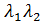= 0 , то – парабола.

Пример 1.Определить тип кривой второго порядка , заданной уравнением: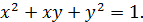

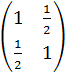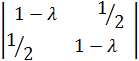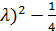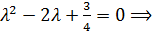
Решение.Составим симметрическую матрицу из коэффициентов при переменных А = , характеристическое уравнение на собственные числа имеет вид = ( 1 - = 0 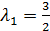, 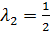. 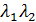= 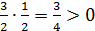. Ответ.Кривая - эллипс.

Пример 2. Определить тип кривой второго порядка : xy = 1.

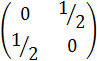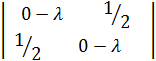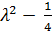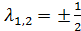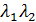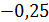
Решение.Матрица А = ; = = 0, Произведение = . Ответ.Кривая - гипербола .