Алгебраические дополнения и миноры
Для наглядности снова раскроем определитель 3-го порядка по правилу треуголь-ника
 =
= 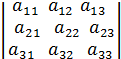 =
= 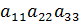 +
+ 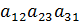 +
+ 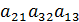 -
- 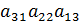 -
- 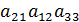 -
-
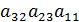 =
= 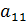 (
( 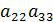 -
- 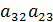 ) +
) + 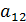 (
( 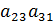 -
- 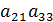 ) +
) + 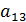 (
( 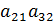 -
- 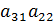 ).
).
Выражения в скобках называются алгебраическими дополнениямиэлементов первой строки и обозначаются:
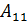 =
= 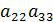 -
- 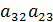 ;
; 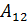 =
= 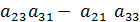 ;
; 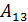 =
= 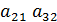 -
- 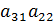
Аналогично, можно сгруппировать члены относительно элементов любой строки или любого столбца и получить алгебраические дополнения элементов этих строк или столбцов. Таким образом , значения определителя равно произведе-
ниям элементов какой – либо строки или столбца на их алгебраические допол-
нения. 6
9). Определитель равен сумме произведений элементов какой-либо строки или столбца на соответствующие алгебраические дополнения элементов этих строк или столбцов.
Находить алгебраические дополнения таким образом нерационально, есть дру-
гой способ.
Определение. Минором данного элемента определителя n-го порядка называ- ется определитель ( n – 1 ) –го порядка , получаемый из данного определителя путём вычёркивания той строки и того столбца на пересечении которых стоит данный элемент.
Минор элемента 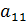 =
= 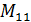 =
= 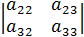 =
= 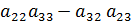 , а минор элемента
, а минор элемента 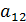 =
= 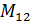 =
= 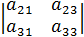 =
= 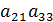 -
- 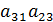 . Сравним эти миноры с алгебраическими дополнениями этих же элементов. Приходим к выводу, что миноры и алгебраические дополнения с точностью до знака совпадают, аналитически это выражается формулой
. Сравним эти миноры с алгебраическими дополнениями этих же элементов. Приходим к выводу, что миноры и алгебраические дополнения с точностью до знака совпадают, аналитически это выражается формулой 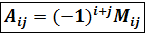
Замечание.Сумма произведений элементов какой –либо строки или столбца на алгебраические дополнения элементов другой строки или столбца равна 0.
Вывод:девятое свойство является способом вычисления определителей порядка выше третьего.
Пример.Применяя свойства , вычислить определитель 4-го порядка.
D = 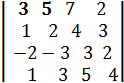
Решение.Произведём следующие действия: 1) из элементов 1-й строки вычтем утроенные элементы 2-й строки; 2) к элементам 3-й строки прибавим удвоенные элементы 2-й строки; 3) из элементов 4-й строки вычтем элементы 2-й строки. Тогда исходный определитель преобразуется к виду
D = 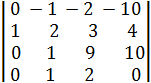 .
.
Разложим этот определитель по элементам 1-го столбца:
D = - 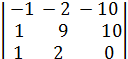 .
.
Прибавляя к элементам 1-й строки элементы 3-й строки и вычитая из элементов 2-й строки элементы 3-й строки, получим
D = -  .
.
Разложим определитель по элементам 1-го столбца:
D = - 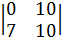 = 70.
= 70.
Определение. Определитель, у которого элементы , стоящие ниже или выше диагонали все нули , имеет диагональный вид.
Примеры.
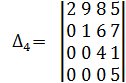
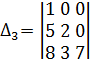 .
.
Дата добавления: 2016-06-05; просмотров: 2430;











