Лекция 4. Общая теория решения систем линейных уравнений.
Рассмотрим систему m линейных уравнений с n неизвестными

Определение. Система (1) называется совместной, если она имеет решение и несовместной, если она не имеет решений.
Определение.Совместная система линейных уравнений называется определённой , если она имеет единственное решение и неопределённой, если она имеет бесчисленное множество решений.
Определение.Две совместные системы уравнений называются равносильными, если каждое решение первой системы является решением второй и обратно.
Теорема Кронекера - Капелли. Кронекер (1823-1891)- немецкий математик. Капелли (1855-1910)-итальянский математик.
Для того , чтобы система линейных уравнений (1) была совместна , необходимо и достаточно , чтобы ранг матрицы системы
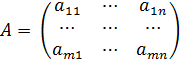 был равен рангу её расширенной матрицы
был равен рангу её расширенной матрицы
B = 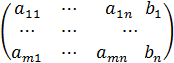 , полученную путём добавления к основной матрице А столбца из свободных членов системы.
, полученную путём добавления к основной матрице А столбца из свободных членов системы.
1). Если r(A) = r(B) = n – числу неизвестных, то система (1) имеет единственное решение.
2). Если же r(A) = r(B) < n , то система (1) имеет бесчисленное множество решений, зависящих от (n – r) параметров (свободных неизвестных).
МЕТОД ГАУССА ( Метод последовательных исключений)
Этот метод продемонстрируем на примере , так как он запрограммирован на электронных машинах и хорошо там просчитывается .
Пример.Решить систему уравнений методом Гаусса.

Установим совместность системы , найдём ранг матрицы, составленной из коэффициентов при неизвестных
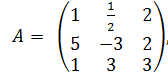 det A =
det A = 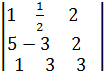 =-9+1+30+6-6-
=-9+1+30+6-6- 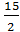
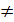 0, значит ранг матрицы А равен 3. Составим расширенную матрицу
0, значит ранг матрицы А равен 3. Составим расширенную матрицу
В = 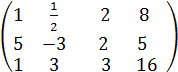 , так как в ней содержится det A
, так как в ней содержится det A 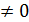 , то rang B также равен 3. Делаем вывод : согласно теореме Кронекера-Капелли r(A)=r(B)=3-числу неизвестных , поэтому система совместна и имеет единственное решение.
, то rang B также равен 3. Делаем вывод : согласно теореме Кронекера-Капелли r(A)=r(B)=3-числу неизвестных , поэтому система совместна и имеет единственное решение.
Решение. Из 1-го уравнения выражаем 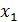 и подставляем во 2-е и 3-е
и подставляем во 2-е и 3-е 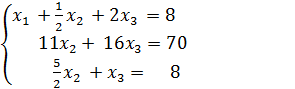 Из 2-го уравнения выражаем
Из 2-го уравнения выражаем 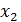 и подставляем в 3-е.
и подставляем в 3-е.
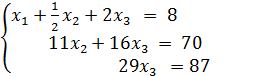 Теперь обратным ходом из 3-го выражаем
Теперь обратным ходом из 3-го выражаем 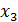 и подставляем во 2-е уравнение, из 2-го выражаем
и подставляем во 2-е уравнение, из 2-го выражаем 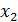 и подставляем 1-е , окончательно получаем:
и подставляем 1-е , окончательно получаем: 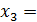 3;
3; 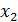 = 2;
= 2; 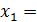 1.
1.
Ответ: 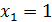 ;
; 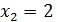 ;
; 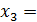 3.
3.
ФОРМУЛЫ КРАМЕРА
ЗАДАЧА.Решить систему 2-х линейных уравнений с 2-мя неизвестными.
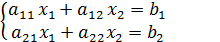
Решение.Умножим обе части первого уравнения на 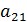 , а 2-го на
, а 2-го на 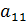 и вычтем из 1-го уравнения 2-е.
и вычтем из 1-го уравнения 2-е.
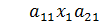 +
+ 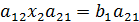
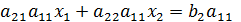
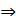
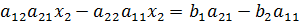
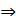
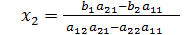 . Числитель этой дроби равен определителю –
. Числитель этой дроби равен определителю –
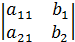 . Знаменатель равен -
. Знаменатель равен - 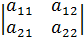 , обозначим
, обозначим  =
= 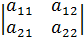 , а через
, а через 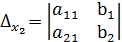 , тогда
, тогда 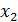 =
= 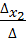 . Аналогичными действиями можно получить
. Аналогичными действиями можно получить 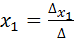 , где
, где 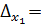
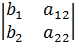 . Решение системы запишем в виде :
. Решение системы запишем в виде :
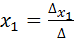 ,
, 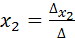 . Для системы , состоящей из трёх уравнений с тремя неизвестными эти формулы примут вид:
. Для системы , состоящей из трёх уравнений с тремя неизвестными эти формулы примут вид:
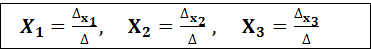 , это и есть формулы Крамера, где
, это и есть формулы Крамера, где
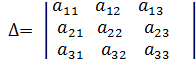 ,
, 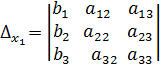 ,
, 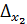 =
= 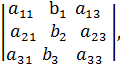
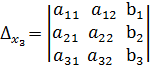 .
.  - главныйопределитель;
- главныйопределитель; 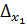 ,
, 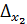 ,
, 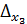 - побочные.
- побочные.
Пример. Решить систему уравнений: 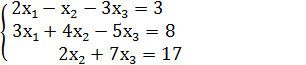
Решение.  =
= 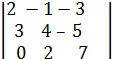 = 79
= 79  0 .Система совместна.
0 .Система совместна. 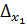 =
= 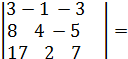 =395,
=395, 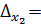
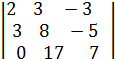 =-158 ,
=-158 , 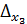 =
= 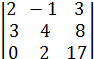 = 237.
= 237.
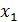 =
= 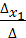 = 5 ;
= 5 ; 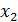 =
= 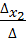 ;
; 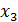 =
= 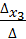 . Ответ.
. Ответ. 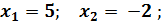
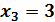 .
.
Из формул Крамера следует :
1). 
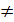 0 система имеет единственное решение.
0 система имеет единственное решение.
2).  = 0 , но хотя бы один из
= 0 , но хотя бы один из 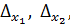
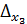
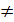 0 , то система не имеет решения.
0 , то система не имеет решения.
3).  =
= 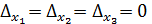 , то система имеет бесчисленное множество решений или совсем не имеет решения.
, то система имеет бесчисленное множество решений или совсем не имеет решения.
18
Дата добавления: 2016-06-05; просмотров: 4418;











