Лекция 2 . Понятие матрицы. Основные операции над матрицами. Собственные числа и собственные векторы матрицы.
Определение.Матрицей называется прямоугольная таблица из m строк и n столбцов элементов некоторого множества.
m 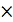 n - порядок матрицы. Если m=n , то матрица называется квадратной , m
n - порядок матрицы. Если m=n , то матрица называется квадратной , m 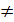 n – прямоугольной. Обозначается:
n – прямоугольной. Обозначается:
A = 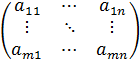 или A =
или A = 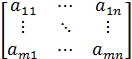 , или A =
, или A = 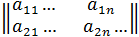
Коротко А = 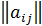 (i =
(i = 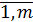 j =
j = 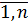 ) , числа
) , числа 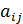 - элементы матрицы.
- элементы матрицы.
( 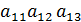 ) - матрица строка;
) - матрица строка; 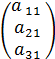 - матрица столбец.
- матрица столбец.

Если m = n , то матрица называется квадратной,если m ≠ n , то матрица прямоугольная.
Определение.Определитель, составленный из элементов квадратной матрицы называется определителем матрицы.
Если матрица
A = 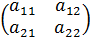 , то определитель
, то определитель 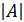 =
= 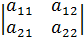
Если 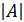 ≠ 0 , то матрица называется невырожденной; если
≠ 0 , то матрица называется невырожденной; если 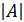 = 0 ,то матрица называется вырожденной.
= 0 ,то матрица называется вырожденной.
A =  – нуль матрица . E =
– нуль матрица . E =  - единичная диагональная матрица.
- единичная диагональная матрица.
Порядок матрицы обозначается так : m  n , где m – количество строк , а n - количество столбцов.
n , где m – количество строк , а n - количество столбцов.
ОСНОВНЫЕ ОПЕРАЦИИ НАД МАТРИЦАМИ
Определение.Две матрицы A и B называются равными ( A = B ) , если они имеют одинаковое число строк и столбцов и их соответствующие элементы совпадают.
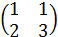 =
= 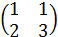 ;
; 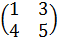 ≠
≠ 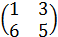 ; ( 1 2 3) ≠
; ( 1 2 3) ≠ 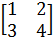 .
.
1). Суммой 2-х матриц A = 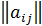 и B =
и B = 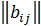 ( i =
( i = 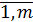 ; j=
; j= 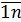 ) называется матрица C =
) называется матрица C = 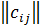 , ( i =
, ( i = 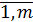 ; j =
; j = 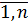 ) ,того же порядка, где
) ,того же порядка, где 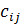 =
= 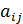 +
+ 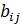 ,т.е. С=A+B.
,т.е. С=A+B.
Если
A = 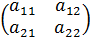 и B =
и B = 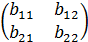 , то С =
, то С = 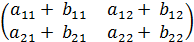 или
или
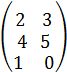 +
+ 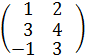 =
= 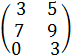
CВОЙСТВА СЛОЖЕНИЯ
а). А + В = В + А.
б). ( А+ В) +С = А + ( В + С ).
2).Умножение матрицы на число.
Определение.Произведением матрицы А = 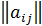 (i =
(i = 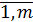 ; j =
; j = 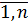 ) на вещественное число
) на вещественное число 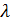 называется матрица С =
называется матрица С = 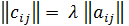 (i=
(i= 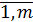 ; j =
; j = 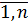 ) , т.е.
) , т.е.
С = 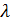 А. Пусть матрица
А. Пусть матрица
А = 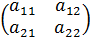 , тогда матрица
, тогда матрица 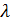 А =
А = 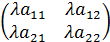 .
.
Дата добавления: 2016-06-05; просмотров: 2045;











