Свойства скалярного произведения.
1° коммутативность: a • b = b •· a.
a • b= │a│·│b│· cos φ= │b│·│a│· cos φ= b • a.
2° условие перпендикулярности: a • b= 0, т.к. a ┴ b или a или b= 0.
1. a ┴ b, φ= 90°, cos 90°= 0, a • b= │a│·│b│·0= 0.
2. a= 0, │a│= 0, a • b= 0 ·│b│· cos φ= 0.
3° (λa)•b= λ(a•b).
(λa)•b= │λa│·│b│· cos φ=λ│a│·│b│· cos φ= λ(a•b).
4° a•(b + c)= a•b + a•c.
a•(b + c)= │a│· 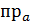 (b + c)= │a│·( пра b + пра c)= │a│·пра b +│a│· пра c=
(b + c)= │a│·( пра b + пра c)= │a│·пра b +│a│· пра c=
= a•b + a•c.
5° скалярный квадрат: а • а= │a│2.
а • а=│a│·│а│· cos 0°=│a│2.
Следствие: 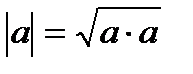 .
.
Скалярное произведение координатных ортов.
i × j= 0, так как i ^ j (из 2°);
i × k= 0, так как i ^ k (из 2°);
k × j= 0, так как k ^ j (из 2°);
i × i=│i│2 = 12=1;
j × j=│j│2 = 12=1;
k × k=│k│2 = 12=1.
Скалярное произведение в координатной форме.
Возьмем два вектора в координатной форме
а= (ах, ау, аz)= axi + ayj + azk, b= (bx, by, bz)= bxi + byj + bzk.
a • b= (axi + ayj + azk )•( bxi + byj + bzk)= axi•bxi + axi•byj + axi •bzk + ayj• bxi +
+ ayj• byj + ayj •bzk + azk •bxi + azk•byj + azk •bzk = ax bx i• i + ax by i•j + ax bz i•k+
+ay bx i• j + ay by j• j + ay bz i• k + az bx i•k + az by k• j + az bz k•k=
= ax bx + ay by + az bz.
Если векторы заданы в координатной форме, то для вычисления скалярного произведения используем формулу:
a • b= ax bx + ay by + az bz.
Приложения скалярного произведения.
1) Угол между векторами:
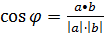 .
.
Ðj - острый, cos j> 0, отсюда следует, что a • b> 0.
Ðj - тупой, cos j< 0, отсюда следует, что a • b< 0.
Ðj= 90°, cos j= 0, отсюда следует, что a • b= 0.
2) Проекция вектора на вектор:
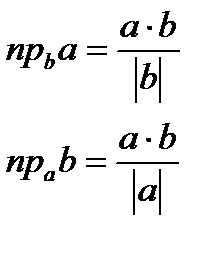 .
.
Дата добавления: 2016-06-05; просмотров: 1696;











