Активная, реактивная и полная мощности пассивного двухполюсника

Разнообразие физических явлений, происходящих в элементах электрических цепей синусоидального тока, усложняет задачу формализации методов анализа этих цепей.

Рассмотрим режим работы источника напряжения, подключенного к пассивному двухполюснику. В общем случае пассивный двухполюсник можно представить эквивалентной схемой замещения в виде последовательного соединения двух элементов: с активным сопротивлением r и реактивным сопротивлением x. Элемент с активным сопротивлением - это резистивный элемент с сопротивлением r, а элемент с реактивным сопротивлением - это индуктивный элемент с индуктивным сопротивлением x_L = wL, если x > 0, или емкостной элемент с емкостным сопротивлением x_С = 1/wС, если x < 0.

Определим мгновенную мощность пассивного двухполюсника, равную мгновенной мощности источника ЭДС при напряжении и токе:

.

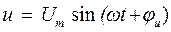
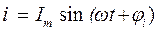Мгновенная мощность равна:

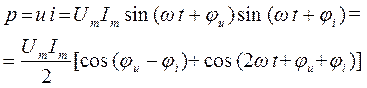
Мгновенные значения тока, напряжения и мощности при индуктивном и емкостном характере комплексного сопротивления двухполюсника показаны на рисунках а) и б) соответственно:

Энергетический процесс в обоих случаях складывается из уже рассмотренных выше энергетических процессов для идеальных элементов. Часть электрической энергии источника поступает в двухполюсник и преобразуется в другие формы энергии. Другой частью энергии источник и двухполюсник периодически обмениваются.

Средняя мощность пассивного двухполюсника за период (равная средней мощности источника) определяется:

.

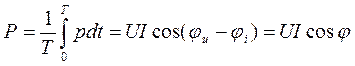Угол сдвига фаз между напряжением и током 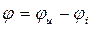зависит от параметров r и x. Последнее выражение определяет активную мощность двухполюсника и источника, которая зависит от действующих значений напряжения и тока, а также от cos j – коэффициента мощности.

Активная мощность двухполюсника измеряется ваттметром. У ваттметра две измерительные цепи, одна из которых включается последовательно с двухполюсником, то есть ток в этой цепи равен току I, протекающему через двухполюсник, а вторая – параллельно с двухполюсником (на его выводы), то есть напряжение в этой цепи равно напряжению U двухполюсника. Чтобы учесть знак угла сдвига фаз j между напряжением и током двухполюсника, измерительные цепи должны быть включены аналогично относительно положительных направлений тока и напряжения. Поэтому один из выводов каждой измерительной цепи имеет отличительное обозначение (как правило, *).

Из треугольников сопротивлений и треугольников напряжений пассивного двухполюсника следует, что коэффициент мощности равен:

.

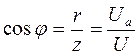Тогда можно получить другое выражение для активной мощности:

.

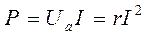Произведение действующих значений напряжения между выводами источника U = E и тока источника I определяет полную мощность источника, равную полной мощности пассивного двухполюсника:

.

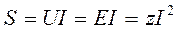Размерности активной мощности и полной мощности совпадают, но для измерения полной мощности выбрана своя единица – вольт-ампер.

Для анализа энергетических процессов в цепи при неполном использовании энергетических возможностей источника вводится понятие о реактивной мощности источника:

.

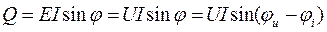Введение реактивной мощности позволяет правильно отобразить совокупность физических процессов, протекающих в реактивных цепях

Из треугольника сопротивлений пассивного двухполюсника следует, что

.

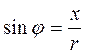После замены sin j в формуле реактивной мощности получим другое выражение для расчета реактивной мощности:

.

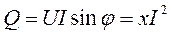Реактивная мощность пассивного двухполюсника может быть положительной и отрицательной в зависимости от знака угла j.

Нетрудно установить связь активной, реактивной и полной мощностей пассивного двухполюсника:

.

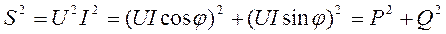Это соотношение удобно интерпретировать геометрически на комплексной плоскости:

Такие треугольники называются треугольниками мощностей. Из подобия треугольников сопротивлений и мощностей следует, что

.

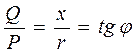Стороны треугольника мощностей связаны между собой зависимостью:

,

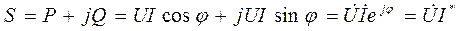где 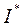– комплексное сопряженное значение тока ,

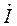S – комплексная мощность.