Нормальное распределение (закон Гаусса)

Распределение непрерывных СВ описывается специальными законами, среди которых, наиболее важным является нормальное распределение (закон Гаусса). Нормальное распределение выступает в качестве предельного закона, к которому при определённых условиях приближаются другие теоретические распределения.

НСВ Х распределена по нормальному закону Х~N(a;σ), если её функция плотности распределения имеет вид:

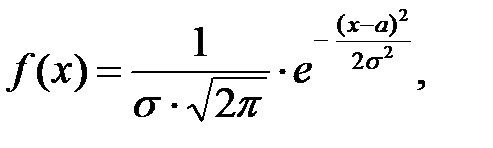
где а и σ>0 – параметры нормального распределения.

Свойства функции плотности вероятности f(x)

нормального распределения

а) f(x)>0, график расположен выше оси х.

б) прямая х=а – ось симметрии графика f(x).

в) 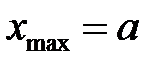– единственная точка экстремума функции f(x).

г) 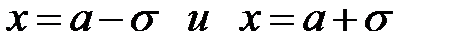– точки перегиба графика f(x).

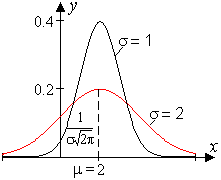График f(x) - кривая нормального распределения (кривая Гаусса)

- имеет идеально симметричную форму,

коэффициенты асимметрии и эксцесса

для нормального распределения равны нулю.

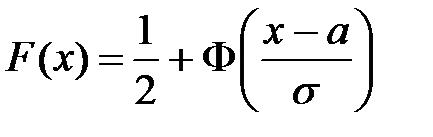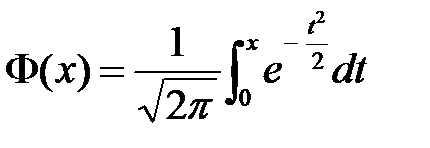Функция распределения СВ Х~N(a;σ) находится по формуле: , где - функция Лапласа.

При а=0 и σ=1, нормальное распределение называется стандартным.

Плотность вероятности стандартной СВ имеет вид: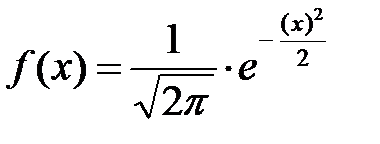

Стандартное нормальное распределение часто используется в статистических исследованиях, поэтому значения функции Лапласа табулированы.

Пример. Случайная величина Х задана функцией плотности вероятности: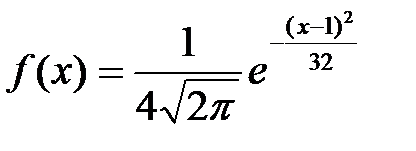

Доказать, что СВ Х распределена по нормальному закону

Найти М(х), D(х), σ(x). Построить схематически график f(x).

Решение. Функция f(x) имеет вид функции плотности вероятности для нормального распределения с параметрами, а=1 и σ=4. Для нормально распределённой СВ Х М(х)= а=1, D(х)=σ²=16, σ(x)=σ=4.

Для построения графика f(x) найдём координаты вершины графика и точек перегиба f(x)

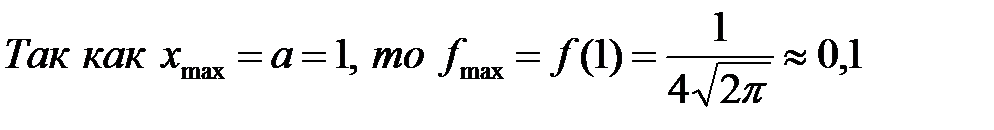; 0,06

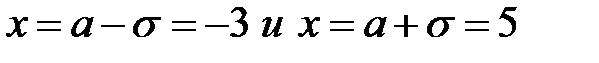– 1 х

точки перегиба графика): f(5= f(-3)=0,06