Числовые характеристики системы двух СВ
 1. Ковариация cov(X,Y) или корреляционный момент - математическое ожидание произведения отклонений этих СВ от их математических ожиданий .
1. Ковариация cov(X,Y) или корреляционный момент - математическое ожидание произведения отклонений этих СВ от их математических ожиданий .
2. Коэффициент корреляции– это количественная мера взаимосвязи двух переменных: 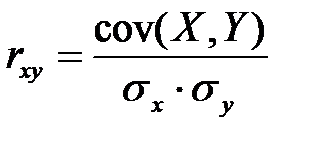 ,
,
гдеσx и σyсредние квадратические отклонения X и Y.
Свойства коэффициента корреляции:
а) коэффициент корреляции по абсолютной величине
не превосходит 1: -1≤ 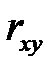 ≤1;
≤1;
б) чем ближе 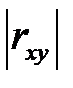 к единице, тем большая вероятностная (стохастическая) зависимость между X и Y (сила связи). Количественной мере тесноты связи
к единице, тем большая вероятностная (стохастическая) зависимость между X и Y (сила связи). Количественной мере тесноты связи 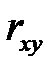 можно дать качественную оценку (шкала Чеддока):
можно дать качественную оценку (шкала Чеддока):
Количественная мера тесноты связи 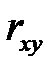
| Качественная характеристика силы связи |
| 0,1 - 0,3 | Слабая |
| 0,3 - 0,5 | Умеренная |
| 0,5 - 0,7 | Заметная |
| 0,7 - 0,9 | Высокая |
| 0,9 - 0,99 | Весьма высокая |
в) знак 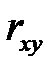 определяет направление связи. Если
определяет направление связи. Если 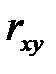 >0, то между Х и Y прямая зависимость (чем больше Х, тем больше Y), если
>0, то между Х и Y прямая зависимость (чем больше Х, тем больше Y), если 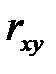 <0, то зависимость между Х и Y обратная (чем больше Х, тем меньше Y);
<0, то зависимость между Х и Y обратная (чем больше Х, тем меньше Y);
г) если Х и Y независимы, то 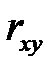 =0;
=0;
д) если Х и Y связаны линейной зависимостью, т.е. Х= а Y + в,
где а ≠ 0, то 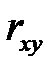 = 1 или
= 1 или 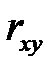 = -1 (
= -1 ( 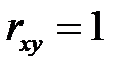 при а > 0 и
при а > 0 и 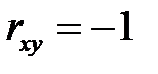 при а < 0);
при а < 0);
е) если 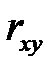 = 1 или
= 1 или 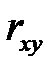 = -1, то Х и Y связаны линейной зависимостью.
= -1, то Х и Y связаны линейной зависимостью.
Пример: Найти коэффициент корреляции СВ X и Y, если закон распределения двумерной СВ (X; Y) задан таблицей:
| X\Y | |||
| 0,1 | 0,3 | 0,2 | |
| 0,2 | 0,1 | 0,1 |
а) определим законы распределения одномерных СВ X и Y.
| Х | ||
| Р | 0,6 | 0,4 |
| Y | |||
| Р | 0,3 | 0,4 | 0,3 |
б) найдём числовые характеристики одномерных СВ X и Y.
М(Х)=0  0,6+1
0,6+1  0,4=0,4; М(Y)=0
0,4=0,4; М(Y)=0  0,3+1
0,3+1  0,4+2
0,4+2  0,3=1;
0,3=1;
D(X)=02  0,6+12
0,6+12  0,4-0,42=0,4-0,16=0,24;
0,4-0,42=0,4-0,16=0,24; 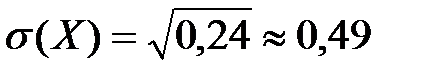 ;
;
D(Y)=02  0,3+12
0,3+12  0,4+22
0,4+22  0,3-12=0,4+1,2-1=0,6;
0,3-12=0,4+1,2-1=0,6; 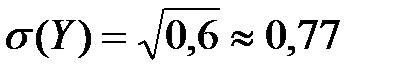 ;
;
в) вычислим
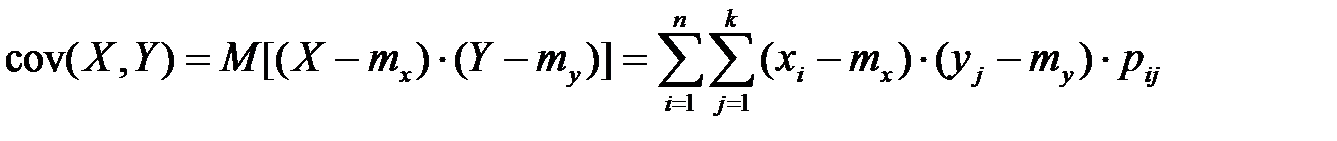 ,
,
где 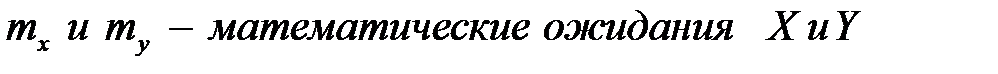 .
.
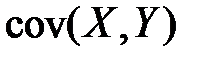 =(0-0,4)
=(0-0,4)  (0-1)
(0-1)  0,1+(0-0,4)
0,1+(0-0,4)  (1-1)
(1-1)  0,3+(0-0,4)
0,3+(0-0,4)  (2-1)
(2-1)  0,2+
0,2+
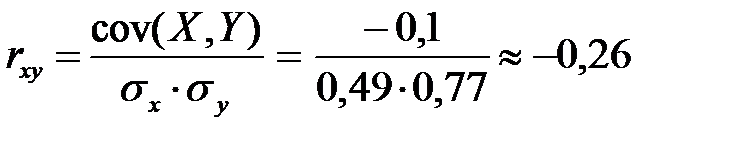 +(1-0,4)
+(1-0,4)  (0-1)
(0-1)  0,2+(1-0,4)
0,2+(1-0,4)  (1-1)
(1-1)  0,1+(1-0,4)
0,1+(1-0,4)  (2-1)
(2-1)  0,1= - 0,1
0,1= - 0,1
Вывод: существует слабая отрицательная корреляционная зависимость между случайными величинами X и Y
Дата добавления: 2016-06-05; просмотров: 2006;











