Построение эпюр изгибающих моментов и поперечных сил

Балкой называется брус, претерпевающий деформацию поперечного изгиба.

Прямой изгиб – вид деформации, при котором внешние усилия приложены к брусу перпендикулярно к его продольной оси и действуют в плоскости, совпадающей с одной из главных плоскостей инерции бруса (если центр тяжести сечения и центр изгиба совпадают). При этом в поперечных сечениях бруса возникают изгибающий момент и поперечная сила, действующие в той же плоскости, что и внешние силы. Такой изгиб называется прямым поперечным. Если в сечениях бруса возникает только изгибающий момент, а поперечная сила равна нулю, то такой изгиб называется прямым чистым изгибом.

Если центр тяжести сечения и центр изгиба не совпадают, то при прямом изгибе плоскость действия внешних сил проходит через центр изгиба параллельно одной из главных осей инерции поперечного сечения.

Центром изгиба называется точка, находящаяся в плоскости поперечного сечения бруса, в которой приложенная сила перпендикулярна продольной оси, не вызывает кручения сечения.

При построении эпюр внутренних усилий (графиков их изменения по длине бруса) используется метод сечений, описанный в главе 1.

1. На брусе выделяем грузовые участки. Часть бруса, в пределах которой закон изменения внутреннего усилия описывается одним аналитическим выражением, называется грузовым участком. Внешними признаками границ грузовых участков являются:

– точки приложения сосредоточенных сил и моментов;

– места расположения опор;

– места начала и конца действия распределенных нагрузок;

– места изменения интенсивности распределенной нагрузки.

– места изломов оси.

2. В пределах каждого грузового участка проводим сечения, перпендикулярные продольной оси бруса, на расстоянии х_i от начала данного грузового участка или от начала бруса, т.е. начало координат совмещаем с началом каждого грузового участка или оставляем неподвижным на одном из краев бруса (рис. 7.1а).

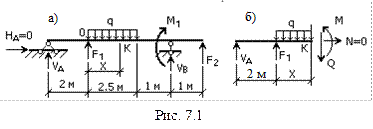
3. Отбрасываем любую часть (лучше ту, на которую действует больше сил).

4. Заменяем действие отброшенной части на оставшуюся положительными изгибающим моментом и поперечной силой (рис. 7.1б). При этом используем следующее правило знаков: изгибающий момент в рассматриваемом сечении считается положительным, если от нагрузки, действующей на рассматриваемую отсеченную часть стержня, он стремится растянуть в этом сечении нижние продольные волокна, и отрицательным, если стремится растянуть верхние волокна (рис. 7.2а).

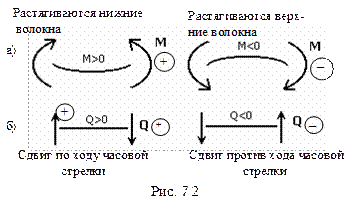
Ординаты эпюр изгибающих моментов принято откладывать со стороны растянутых волокон. Таким образом, знаки для изгибающих моментов в дальнейшем будем использовать только при их вычислении в различных сечениях балки и не указывать на эпюрах изгибающих моментов.

Поперечная сила в сечении считается положительной, если стремится сдвинуть отсеченную часть по ходу часовой стрелки и отрицательной – если против хода часовой стрелки (рис. 7.2б).

5. Составив уравнения равновесия для оставшейся части, определим значения изгибающего момента и поперечной силы в рассматриваемом сечении К (см. рис. 7.1б):

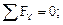
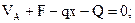
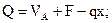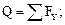или (7.1)

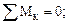
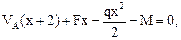отсюда

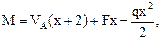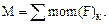или (7.2)

Выражения (7.1) и (7.2) позволяют сформулировать следующие практически полезные рабочие правила:

1. Поперечная сила в любом сечении бруса численно равна алгебраической сумме проекций всех внешних сил, приложенных к одной (рассматриваемой) части бруса на ось, перпендикулярную оси бруса в данном сечении.

2. Изгибающий момент в любом поперечном сечении бруса численно равен алгебраической сумме моментов всех внешних сил, приложенных к одной (рассматриваемой) части бруса относительно центра тяжести рассматриваемого сечения (для плоских систем) или относительно оси, проходящей через центр тяжести данного сечения и перпендикулярной плоскости действия сил (для пространственных систем).

Для выявления опасных сечений, где действуют наибольшие значения изгибающих моментов и поперечных сил, необходимо строить графики их функций т.е. эпюры. Порядок построения эпюр М и Q рассмотрен на ряде примеров при расчете балок на прочность в п. 7.4.