Кручение бруса круглого сечения в упругопластической стадии

Заменим реальную криволинейную диаграмму сдвига (на рис. 6.9 она показана пунктирной линией) – диаграммой Прандтля при сдвиге, т.е. будем считать, что при τ < τ_S ( 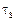– предел текучести при сдвиге) справедлив закон Гука и материал деформируется линейно-упруго. При напряжениях τ = τ_S возникают пластические деформации сдвига, значения которых не­огра­ниченны, а напряжения остаются постоянными и равными τ_S.

Выясним, как будет видоизменяться эпюра касательных напряжений в сечении при постепенном возрастании крутящего момента М_t с учетом упругопластической работы материала.

В упругой стадии напряжения τ распределены вдоль диаметра бруса по линейному закону. При возрастании момента М_t пропорционально возрастают и все напряжения. Конец этой стадии определяет равенство

τ_max = 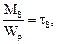(6.25)

когда в точках по краю сечения начинает появляется текучесть (рис. 6.10а). Крутящий момент, соответствующий данному состоянию, обозначим М_S и получим из соотношения (6.25):

М_S = τ_SW_ρ = τ_S 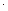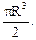(6.26)

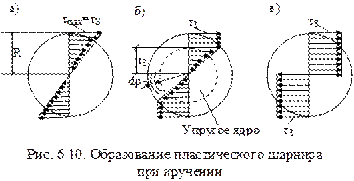
При дальнейшем возрастании крутящего момента пластическая зона будет все больше проникать вглубь сечения бруса (рис. 6.10б), а все сечение разделится на 2 зоны: упругое ядро, где t £ t_S с радиусом r_S и пластическую кольцевую зону r_S £ r £ R, где t = t_S. Суммарный крутящий момент представим как сумму:

М_t = M_t1 + M_t2, (6.27)

где момент упругого ядра М_t1 = t_S 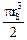(6.28)

найден по формуле (6.26) (R заменено на r_S), а момент пластической кольцевой зоны равен

М_t2 = 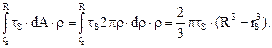(6.29)

При вычислении момента пластической кольцевой зоны элементарная площадь dA равна площади кольца толщиной d 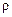, т.е. dA = 2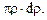

Из формулы (6.29) видно, что при r_S ® 0 пластическая зона стремится охватить все сечение (рис. 6.10в) и внутренний момент стремится к своему предельному значению:

М_пред = 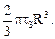(6.30)

Поперечное сечение стержня, в котором во всех точках возникают пластические деформации, называется пластическим шарниром. Cтержень превращается как бы в пластический механизм, в котором углы закручивания неограниченно растут при постоянном моменте М_пред.

Соотношение 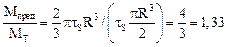показывает, что от момента первого появления пластических деформаций в наиболее напряженных точках бруса до полного исчерпания несущей способности крутящий момент должен возрасти в 1,33 раза, то есть это соотношение выражает резерв несущей способности за счет учета упругопластических свойств материала.

6.6. Контрольные вопросы по теме

1. При каком нагружении прямой брус испытывает только деформацию кручения?

2. Как определяется величина крутящего момента в любом сечении бруса? Каков порядок построения эпюр крутящих моментов?

3. Какие напряжения возникают в поперечном сечении бруса при деформации кручения и как они определяются?

4. Как распределены напряжения в сечении при кручении бруса круглого сечения?

5. Запишите условие прочности при кручении.

6. Каков порядок подбора размеров поперечного сечения бруса при кручении по условию прочности?

7. Что называется полярным моментом сопротивления поперечного сечения?

8. Как определяется полярный момент сопротивления для круглого сплошного и кольцевого сечений?

9. Какие задачи кручения брусьев решаются с использованием условия прочности?

10. Что называется жесткостью сечения при кручении?

11. Как определяется взаимный угол закручивания сечений на участке бруса длиной l?

12. Как определяется относительный угол закручивания?

13. Как определяется полный угол закручивания сечения по отношению к неподвижному или начальному сечению?

14. Как записываются условия жесткости при кручении через полный и относительный углы закручивания?

15. Поясните порядок подбора сечений при кручении из условий жесткости.

16. Каков порядок решения статически неопределимых задач при кручении?

17. Как распределяются касательные напряжения при кручении бруса прямоугольного сечения?

18. Запишите условие прочности при кручении бруса прямоугольного поперечного сечения.