А. Построение эпюр М и Q

1. В пределах грузовых участков 1, 2, 3 (рис. 7.7а) проводим сечения на расстоянии x_i от начала каждого участка. При этом рассматриваем правую, свободную от опоры, часть балки, а левую отбрасываем.

Заменяя действие отброшенной части неизвестными

положительными поперечной силой Q_i(x_i) и изгибающим моментом М_i(x_i) и рассматривая равновесие выделенной части балки, находим выражения внутренних усилий на участках.

При построении эпюр М и Q и их проверке используем дифференциальные зависимости Д.И. Журавского между М, Q и q:

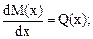
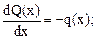
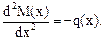(7.17)

В зависимостях (7.11) перед q ставится знак "минус", если распределенная нагрузка направлена вниз.

1-й грузовой участок (рис. 7.8)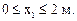

Составим уравнения равновесия для 1-го участка.

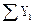= 0; Q₁(x₁) – qx₁ + F = 0; 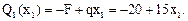Так как Q₁(x₁) – линейная функция, то для построения эпюры Q на этом участке достаточно рассмотреть два сечения:

х₁ = 0 м, Q₁(0) = – 20 кН;

х₁ = 2,0 м, Q₁(2) = 10 кН.

Строим эпюру Q из которой видно (см. рис. 7.7е), что на первом участке эпюра поперечных сил имеет нулевую ординату. В соответствии с дифференциальной зависимостью (7.17) между М и Q ( 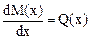) эпюра изгибающих моментов на этом участке будет иметь экстремум.

Приравнивая Q₁(х₁) к нулю при х₁ = х₀, получим:

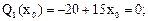
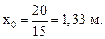
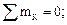–М₁(х₁) – q 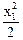+ F×x₁ = 0;

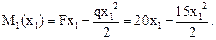
Функция М₁(х₁) – квадратичная, поэтому для построения графика этой функции на данном участке (эпюры М), находим не менее трех значений изгибающего момента:

х₁ = 0 м, М₁(0) = 0 кН×м;

х₁ = х₁ = 1,33 м, М₁(х₀) = M_extr = 13,3 кН×м;

х₁ = 2,0 м, М₁(2) = 10 кН×м.

По найденным значениям строим эпюру М на первом участке под эпюрой поперечных сил. Изгибающие моменты откладываем со стороны растянутых волокон, т.е. "плюс" – вниз (растягиваются нижние волокна), "минус" – вверх (растягиваются верхние волокна) см. (рис. 7.7е, ж).

Аналогично построим эпюры на 2-м и 3-м грузовых участках:

2-й участок (рис. 7.9):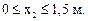

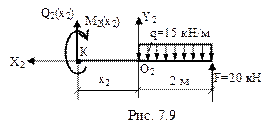
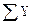= 0; Q₂(x) – q 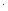2 + F = 0;

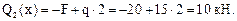
Эпюра Q постоянна по длине данного участка.

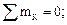– М₂ (х₂) – q 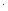2 (х₂ + 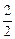) + F (x₂ + 2) = 0;

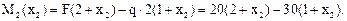
Изгибающий момент на данном участке изменяется по линейному закону:

х₂ = 0 м,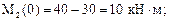

х₂ = 1,5 м,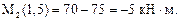

3-й участок (рис. 7.10):

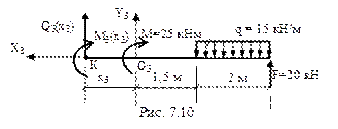
Рассматривая 3-й участок также вырежем правую часть балки. Начало локальной системы координат поместим в начале 3-го участка.

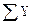= 0; Q₃(x₃) – q 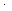2 + F = 0;

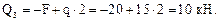
Эпюра Q постоянна по длине участка.

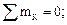–М₃(х₃) – М – q×2(х₃ + 1 + 1,5) + F × (x₃ + 3,5) = 0;

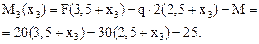
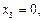
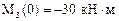(знак "минус" означает, что растягиваются верхние волокна);

х₃ = 1 м,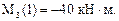

Эпюры М и Q, построенные по результатам расчётов, показаны на рис. 7.7е, ж.

Б. Подбор сечения

Из эпюр М и Q имеем: 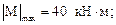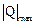= 20 кН.

1. Балка прямоугольного сечения (см. рис. 7.7б):

R = 10 МПа, R_s = 5 МПа, h = 4b.

Из условия прочности (7.2) определим требуемую величину осевого момента сопротивления при :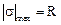

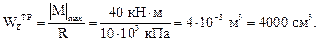
Осевой момент сопротивления для прямоугольного сечения при заданных соотношениях сторон определится по формуле:

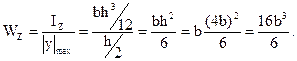
Приравняем 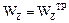и найдем размер сечения b:

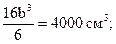
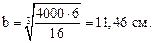
Округляя в большую сторону, примем:

b = 11,5 см, h = 4b = 4 11,5 = 46 см.

Проверим прочность подобранного сечения по нормальным и касательным напряжениям.

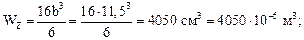
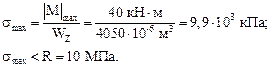
Прочность по нормальным напряжениям обеспечена. Недонапряжение в 1 % объясняется округлением размера сечения b в большую сторону.

Для проверки прочности по касательным напряжениям используем формулу (7.11):

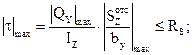
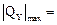20 кН, (из эпюры Q);

I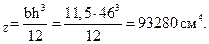

Наибольшие касательные напряжения для прямоугольного сечения возникают в точках, лежащих на центральной оси Z, так как S 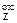для полусечения (отсечение проводится через точку К,находящуюся на центральной оси Z)имеет максимальное значение (рис. 7.11в):

S 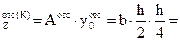11,5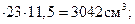

b 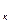= b = 11,5 см. А^отс = b 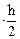; y = .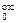

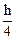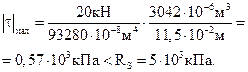
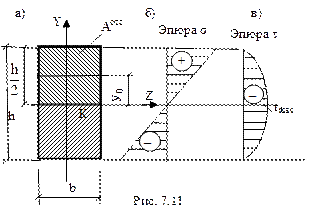
Прочность по касательным напряжениям обеспечена с большим запасом.

2. Балка сплошного круглого сечения, материал – дерево,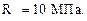

Требуемый осевой момент сопротивления берем из предыдущего расчета, так как он не зависит от формы сечения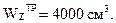

Осевой момент сопротивления для круглого сечения:

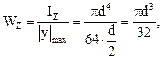где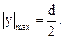

Из условия 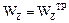имеем:

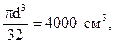отсюда –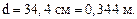

Округляя, примем d = 0,35 м.

Проверим прочность подобранного сечения по нормальным напряжениям:

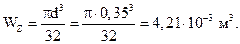
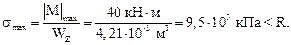
Прочность балки по нормальным напряжениям обеспечена. Небольшое недонапряжение (–5 %) объясняется округлением диаметра в большую сторону.

Наибольшая ширина данного сечения d находится на центральной оси, значит максимальные касательные напряжения будут небольшими, поэтому для данного сечения проверку по касательным напряжениям можно не производить.

3. Балка из прокатного двутавра (см. рис. 7.7г).

Из условия прочности по нормальным напряжениям определяем требуемое значение осевого момента сопротивления:

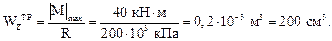
Из таблицы сортаментов по ГОСТ 8239-89 для стального проката находим двутавр, имеющий близкий к требуемому осевой момент сопротивления:

Двутавр № 20,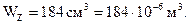

Проверим прочность этого двутавра:

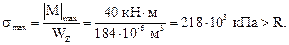
Определим процент перенапряжения.

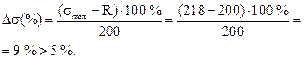
Такая величина перенапряжения считается недопустимой, поэтому проверим прочность двутавра № 22.

Для этого двутавра из сортамента имеем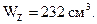

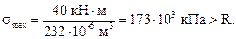
Имеет место недонапряжение

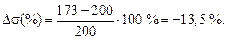
Окончательно выбираем двутавр № 22.

Проверим прочность подобранного сечения по касательным напряжениям.

Наибольшие касательные напряжения будут в точках сечения, лежащих на центральной оси, так как статический момент полусечения имеет максимальное значение, а толщина в этом месте – минимальная.

Для двутавра № 22 из таблицы сортаментов для прокатных двутавров (ГОСТ 8239-89) получаем:

I ;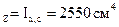

b_К = s_c = 5,4 мм = 0,54 см;

S 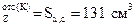– статический момент полусечения.

Тогда

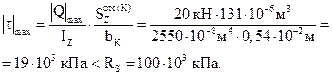
Прочность балки по касательным напряжениям обеспечена с большим запасом.

4. Балка из стальной трубы (см. рис. 7.7д)

R = 200 МПа; R_S = 100 МПа;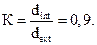

Из предыдущего, третьего пункта, имеем:

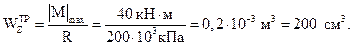
Для кольцевого поперечного сечения:

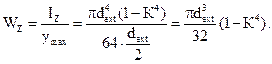
Из условия: W_Z = W 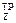определяем наружный диаметр d_ext:

200 см³ =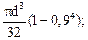

d_ext =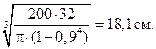

Округляя, примем d_ext = 18 см; d_int = 0,9d_ext = 0,9 18 = = 16,2 см.

Проверим подобранное сечение по нормальным и касательным напряжениям:

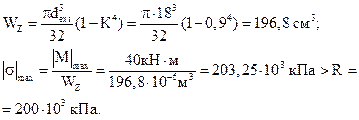
Относительная величина перенапряжения составляет:

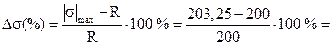
= 1,6 % < 5 %, что допустимо и объясняется округлением требуемого диаметра в меньшую сторону.

Проверяем прочность поперечного сечения по касательным напряжениям. Опасной является точка, лежащая на центральной оси Z, так как для этой точки статический момент полусечения достигает максимального значения, а ширина сечения имеет минимальную величину. Для проверки прочности используем формулу (7.11):

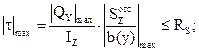
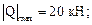
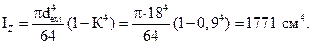
Ширина сечения на уровне центральной оси b_К определится как разность диаметров: b_К = d_ext – d_int = 18 – 16,2 = 1,8 см.

Статический момент отсеченной части сечения выше центральной оси Z определим как разность статических моментов большего и меньшего полукругов:

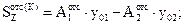
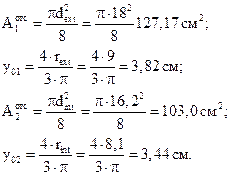
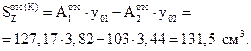
Максимальное касательное напряжение составляет:

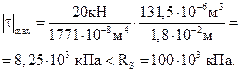
Условие прочности по касательным напряжениям выполняется с большим запасом.

ПРИМЕР 7.2

Для балки, изображенной на рис. 7.12а, требуется:

– построить эпюры М и Q;

– подобрать размеры стальных составных сечений в двух вариантах (по рис. 7.12г, д).

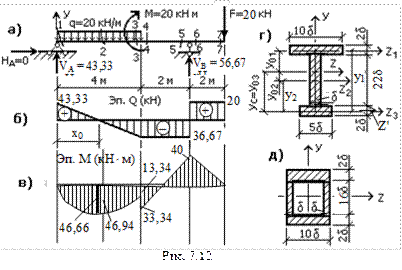
РЕШЕНИЕ