И построение эпюры крутящих моментов

1. Статическая сторона задачи.

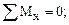
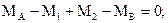
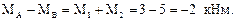
Здесь М_А и М_В – опорные реакции в заделках, действующие в плоскостях, перпендикулярных оси стержня. Их направление выбрано произвольно.

Получили одно уравнение, содержащее два неизвестных, т.е. рассматриваемая задача один раз статически неопределима.

2. Геометрическая сторона задачи.

Для получения дополнительного уравнения рассмотрим условие совместности деформаций отдельных участков.

Определим полный угол закручивания правого концевого сечения бруса по отношению к левому сечению. Он определяется как сумма углов закручивания трех участков и равен нулю.

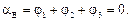
3. Физическая сторона задачи.

Используем закон Гука при кручении для определения j_i:

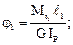
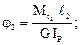
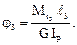
Методом сечений получим выражения для определения крутящих моментов 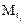из условия равновесия правой отсеченной части:

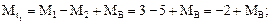
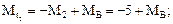
М_t3 = М_В.

Эти выражения подставим в соотношение a_В = j₁ + j₂ + j₃ = 0:

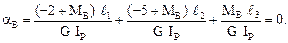
Отсюда найдем значение опорной реакции M_B:

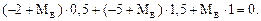
М_В = 2,83 кН·м.

4. Построение эпюры крутящих моментов.

Зная величину опорной реакции, определяем значения крутящих моментов на всех грузовых участках:

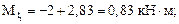
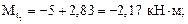
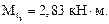
Эпюра 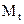изображена на рис. 6.8б.

Б. Подбор сечения

Используя условие прочности при кручении по формуле (6.4) определяем требуемый полярный момент сопротивления поперечного сечения.

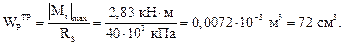
Полярный момент сопротивления круглого сплошного сечения определяется по формуле (6.6):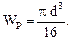

Из равенства 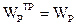определяем d:

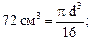d = 7,17 см.

Округляя по ГОСТ 2590-88, примем d = 7,2 см.

Проверим прочность по формуле (6.4):

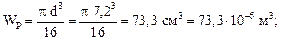
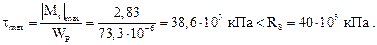
Недонапряжение 3,5 % объясняется округлением требуемого диаметра в большую сторону.