Статически неопределимые задачи при деформации кручения

Как было отмечено ранее, статически неопределимыми называются брусья и системы, внутренние усилия или реакции опор в которых нельзя определить с помощью одних лишь уравнений равновесия. Поэтому при их расчете необходимо составлять дополнительные уравнения – уравнения совместности деформаций или перемещений. Число дополнительных уравнений, необходимых для расчета системы, характеризует степень ее статической неопределимости.

Важным этапом расчета статически неопределимых систем является составление дополнительных (к уравнениям равновесия) уравнений перемещений. Способ их составления поясним на следующем примере.

Рассмотрим стержень, защемленный обоими концами и нагруженный моментом М_Х, действующим в плоскости, перпендикулярной продольной оси стержня (рис. 6.7).

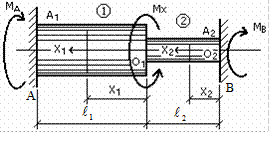
Рис. 6.7

В этом случае в заделках могут возникать только опорные моменты М_А и М_В относительно продольной оси, которые требуется определить. Направления неизвестных опорных реакций показываются произвольно.

Статическая сторона задачи для определения этих неизвестных дает только одно уравнение равновесия:

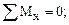
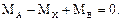(6.20)

Получили одно уравнение с двумя неизвестными, значит степень статической неопределимости данной задачи равна единице. Для составления дополнительного уравнения рассмотрим геометрическую сторону задачи, т.е. составим условие совместности деформаций: полный угол закручивания сечения правого конца бруса (сечения В) по отношению к левому защемленному концу равен нулю, т.е.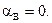

Полный угол закручивания 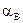равен сумме углов закручивания двух участков:

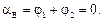(6.21)

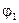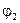Физическая сторона задачи. Углы закручивания отдельных участков и определим по формуле (6.11):

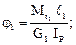
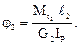(6.22)

В этих формулах выражения для М_t1и M_t2записываем по методу сечений, рассматривая правую отсеченную часть:

M_t1 = M_B – M_X; M_t2 = M_B. (6.23)

Подставляя выражения (6.22) с учетом (6.23) в уравнение (6.21), получим:

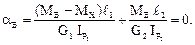
Отсюда при 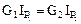имеем: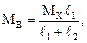

В случае 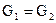и 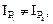получаем

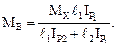(6.24)

ПРИМЕР 6.3

Брус, изображенный на рис. 6.8а, защемлен с двух концов:

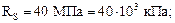
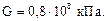
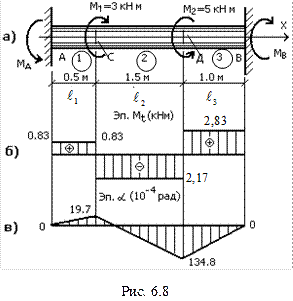
Требуется:

– определить реакции опор и построить эпюры крутящих моментов;

– подобрать диаметр бруса сплошного круглого сечения;

– построить эпюру углов закручивания сечений.

РЕШЕНИЕ