Введение. Математическое программирование.
Исследование операций– прикладное направление кибернетики, используемое для решения организационных и экономических задач (например, задач распределения ресурсов, управления запасами, упорядочения и согласования и др.). Главный метод – системный анализ целенаправленных действий (операций) и объективная (в частности, количественная) сравнительная оценка возможных результатов этих действий. Исследование операций основывается на аппарате математического программирования, теории массового обслуживания, математической статистике, теории игр и др.
Данное научное направление сформировалось во время второй мировой войны, прежде всего для планирования военных операций и их обеспечения, откуда и появилось название «исследование операций».
Математическое программирование – область математики, разрабатывающая теорию и численные методы решения многомерных экстремальных задач с ограничениями, т. е. задач на экстремум функции многих переменных с ограничениями на область изменения этих переменных.
Функцию, экстремальное значение которой нужно найти в условиях возможностей процесса, называют целевой функцией, показателем эффективности или критерием оптимальности. Возможности процесса формализуются в виде системы ограничений.
Модель задачи математического программирования включает:
- совокупность неизвестных величин, действуя на которые, систему можно совершенствовать. Их называют планом задачи (вектором управления, решением, управлением, стратегией, поведением и др.);
- целевую функцию (функцию цели, показатель эффективности, критерий оптимальности, функционал задачи и др.). Целевая функция позволяет выбирать наилучший вариант из множества возможных. Наилучший вариант доставляет целевой функции экстремальное значение. Это может быть прибыль, объем выпуска или реализации, затраты производства, издержки обращения, уровень обслуживания или дефицитности, число комплектов, отходы и т. д.;
- набор условий или ограничений. Эти условия следуют из ограниченности ресурсов предприятия, из особенностей производственных и технологических процессов. Ограниченными могут быть материальные, финансовые и трудовые ресурсы, возможности технического, технологического и научного потенциала.
Математически ограничения выражаются в виде уравнений и неравенств. Их совокупность образует область допустимых решений. План, удовлетворяющий системе ограничений задачи, называется допустимым. Допустимый план, доставляющий функции цели экстремальное значение, называется оптимальным. Оптимальное решение не обязательно является единственным, возможны случаи, когда оно не существует или имеется бесчисленное множество оптимальных решений.
Задача математического программированияформулируется следующим образом: найти значения переменных x1, x2,…, xn, доставляющие максимум (минимум) заданной целевой функции y = f (x1, x2,…, xn) при условиях:
 gj(x1, x2, …, xn) £ (³, =)bj, (j =
gj(x1, x2, …, xn) £ (³, =)bj, (j = 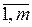 ).
).
Различают два вида задач математического программирования:
- задачи линейного программирования (целевая функция у и ограничения gi линейны относительно переменных х).
- задачи нелинейного программирования (целевая функция у и (или) ограничения gi имеют разного рода нелинейности).
Дата добавления: 2018-11-26; просмотров: 1206;











