Статистическое определение вероятности
Использование классического определения наталкивается на ряд трудностей при решении некоторых задач. Часто это связано с тем, что
1) невозможно представить результат испытания в виде совокупности элементарных событий. Например: попадание стрелка в цель, выход из строя радио деталей и т.п.
2) Затруднительно указать основания, позволяющие считать события равновозможными (обычно в силу отсутствия симметрии явления). Например: рождение мальчика или девочки; распад атомного ядра; игральная кость с неоднородными гранями.
Пусть проводится большое количество повторных испытаний, при неизменных условиях. В каждом из этих испытаний некоторое событие А может произойти или нет. Обозначим через m – число появлений события А в n независимых испытаниях.
Отношение числа наступлений события А к общему числу всех фактически проведенных испытаний, называют относительной частотой или частостью события А и обозначают
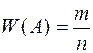
Было замечено, что относительная частота обладает некоторой устойчивостью, которая заключается в том, что при достаточно большом числе испытаний она сохраняет почти постоянную величину, причем большие отклонения тем реже, чем многочисленнее проводимые испытания.
Для иллюстрации этого факта приведем официальные данные шведской статистики о частоте рождаемости девочек в 1935 году по месяцам, взятые из книги Г.Крамера «Математические методы в статистике»: 0,486 0,489 0,490 0,471 0,478 0,482 0,462 0,484 0,485 0,491 0,482 0,479.
Видно, что частости колеблются около числа 0,482.
Оказывается, что для тех случаев, к которым применимо классическое определение вероятности, колебание относительной частоты происходит около вероятности P события.
Имеется огромный опытный материал, подтверждающий этот факт. Приведем эксперимент с бросанием монеты.
| Экспериментатор | Число бросаний | Число выпадений герба | Число выпадений надписи |
| Ж. Бюффон | 4 040 | 2 048 | 0,5080 |
| К. Пирсон | 12 000 | 6 019 | 0,5016 |
| К. Пирсон | 24 000 | 12 012 | 0,5005 |
Относительная частота колеблется около вероятности P = 0,5.
Приведенные факты дают повод предположить наличие независящей от испытателя закономерности течения явления, которая заключаются в указанном почти постоянстве относительных частот. Эту постоянную, являющуюся объективной числовой характеристикой явления, естественно назвать вероятностью случайного события А.
Итак, будем говорить, что событие А имеет вероятность, если выполнены следующие условия:
а) Можно, по крайней мере принципиально, провести в неизменных условиях неограниченное число независимых друг от друга испытаний, в каждом из которых событие А может произойти или нет.
б) Относительная частота события А для достаточно большой группы испытаний колеблется около некоторого числа (вообще говоря заранее неизвестного).
Таким образом, определенная вероятность называется статистической. В качестве числового значения статистической вероятности можно взять относительную частоту
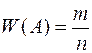 ,
,
или число близкое к ней.
Естественно при этом потребовать, чтобы:
1) вероятность достоверного события была равна 1,
2) вероятность невозможного события – 0,
3) если некоторое событие А является суммой конечного числа несовместных событий Аi, i = 1,2,…,n, имеющих вероятности, то
P(A) = P(A1)+P(A2)+…+P(An)
Данное определение носит лишь описательный, априорный характер. Однако мы сохранили за вероятностью ее объективный, не зависящий от познающего, смысл.
Попытка трактовать вероятность как предел
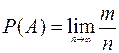
приводила к противоречию с некоторыми основными положениями философии. Не вдаваясь в подробности, укажем лишь на то, что при таком определении вероятность теряет характер объективной числовой характеристики реальных явлений
Действительно, пока не произведем бесконечного числа испытаний, нельзя говорить о наличии вероятности того или иного события. А поскольку этого сделать невозможно, то мы вообще лишены возможности использовать теорию вероятностей.
Дата добавления: 2021-12-14; просмотров: 641;











