Пространство элементарных событий

Будем считать фиксированным комплекс G условий и станем рассматривать некоторую F систему событий A, B, C, …, каждое из которых должно при каждом осуществлении комплекса G произойти или не произойти. Обозначим через U – достоверное событие, а через V – невозможное.

1) Если в результате испытания, из того, что произойдет событие A, следует, что произойдет и событие B, то говорят, что событие A влечет за собой событие B. И обозначают: .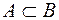

2) Если 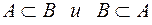, то говорят, что эти события равносильны и записывают А = В.

3) Событие, состоящее в наступлении обоих событий А и В, будем называть их произведением и обозначать: АВ или .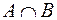

4) Событие, состоящее в наступлении хотя бы одного из событий А или В, называется их суммой и обозначается: .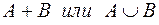

5) Событие, состоящее в том, что событие А наступило, а событие В нет, называют разностью событий А и В.

6) Два события 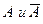называются противоположными, если одно из них обязательно наступит, а другое нет, т.е. выполняются одновременно равенства: .

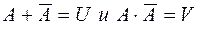Пример: Комплекс условий G состоит в том, что на стол один раз бросается игральная кость. Обозначим:

соб. А – выпадение 6 очков,

соб. В – выпадение 3 очков,

соб. С – выпадение четного числа очков,

соб. D – выпадение числа очков, кратного 3.

Тогда события A, B, C, D связаны следующими соотношениями: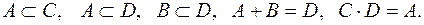

7) События А и В называются несовместными, если их совместное появление невозможно, т.е. АВ = V.

8) Если событие А представимо в виде суммы А = В₁+В₂+ … +В_к и события B_j попарно несовместны, то говорят, что событие А подразделяется на частные случаи. Например, при бросании игральной кости, событие С, состоящее в выпадении четного числа очков подразделяется на три частных случая Е₂, Е₄, Е₆ (выпадение 2, 4, 6 очков).

9) Говорят, что события В₁, В₂, …, B_n образуют полную группу событий, если хотя бы одно из них непременно должно наступить при выполнении данного комплекса условий.

В дальнейшем нас будут интересовать полные группы попарно несовместных событий, т.е. единственно возможных:

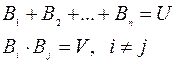
10) Для операций сложения и умножения событий справедливы законы:

Коммутативность: А+В = В+А; АВ =ВА,

Ассоциативность: А+(В+С) =(А+В)+С; А(ВС) = (АВ)С,

Тождества: А+А =А; АА = А,

Дистрибутивность: А(В+С) = АВ+АС;

* А+ВС = (А+В)(А+С).

Классическое определение вероятности случайного события

Классическое определение вероятности опирается на понятие равновозможность событий. «Равновозможность» в свою очередь базируется на симметрии явлений. Например, мы считаем, что выпадение любой из двух граней при бросании монеты равновозможно, если она сделана из однородного материала. Точно так же, мы предполагаем одинаковую возможность выпадения каждой грани при бросании игральной кости. Таким образом, каждый раз, когда мы хотим использовать классическое определение, необходимо проверить равновозможность рассматриваемых событий.

Зададим какую-либо полную группу Q попарно несовместных и равновозможных событий Е₁, Е₂, …,Е_n. Образуем систему F, состоящую из:

а) невозможного события V;

б) достоверного события U = Е₁+Е₂+ … +Е_n;

в) всех событий Е_i, i = 1,2,…,n

г) всех событий А, которые могут быть подразделены на частные случаи, входящие в состав группы Q.

Тогда система F образует алгебраическое поле.

Пусть некоторое событие А поля F подразделяется на m частных случаев, входящих в состав группы Q, т.е. .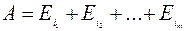

Те элементарные исходы, в результате которых наступает событие А, называют благоприятствующими событию А.

Определение: Вероятностью P(A) события А называется отношение числа m-исходов, благоприятствующих событию А, к числу n всех возможных исходов испытания, образующих полную группу попарно несовместных и равновозможных событий. Записывают

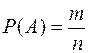
Так, например, вероятность выпадения i очков при бросании игральной кости равна

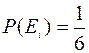
Событие С, состоящее в выпадении четного числа очков, подразделяется на три частных случая, входящих в полную группу равновозможных и попарно несовместных событий

С = Е₂+Е₄+Е₆

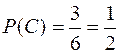
В соответствии с приведенным определением, каждому событию А, принадлежащему построенному полю F, ставится в соответствие определенная вероятность P(A). Таким образом, вероятность P(A) есть функция, определенная на поле F.