Распределение Пуассона

Дискретная СВ X называется распределенной по закону Пуассона, если ее возможные значения 0, 1, 2, …, m, …, а вероятность события (X = m) выражается формулой

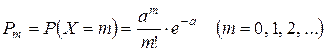, (1.41)

где a > 0. Распределение Пуассона зависит от одного параметра а. Для СВ X, распределенной по закону Пуассона,

M(X) = D(X) = a, (1.42)

т. е. параметр a пуассоновского распределения равен одновременно M(X) и D(X). В этом состоит отличительная особенность распределения Пуассона, которая используется на практике (на основании опытных данных находят оценки для M(X) и D(X); если они близки между собой, то есть основание считать, что СВ X распределена по закону Пуассона).

Пуассоновское распределение является предельным для биномиального при p ® 0, n ® ¥, если np = a = const. Этим распределением можно пользоваться приближенно, если производится большое число независимых опытов, в каждом из которых событие A происходит с малой вероятностью. Примерами СВ X, имеющих распределение Пуассона, являются: число опечаток в большом тексте, число бракованных деталей в большой партии; число a-частиц, испускаемых радиоактивным источником и т. д. При этом считается, что события появляются независимо друг от друга с постоянной интенсивностью, характеризующейся параметром a = np.

Замечание. Имеются специальные таблицы, пользуясь которыми можно найти P_m, зная m и a.

Распределение Пуассона встречается при рассмотрении потоков событий. Потоком событий называется последовательность однородных событий, наступающих одно за другим в случайные моменты времени.

Среднее число событий l, приходящееся на единицу времени, называется интенсивностью потока. Величина l может быть как постоянной, так и переменной l = l(t).

Поток событий называется потоком без последействия, если вероятность попадания того или иного числа событий на какой-либо участок времени не зависит от того, сколько событий попало на любой другой непересекающийся с ним участок.

Поток событий называется ординарным, если вероятность появления на элементарном участке времени Dt двух или более событий пренебрежимо мала по сравнению с вероятностью появления одного события. Ординарный поток событий без последствия называется пуассоновским. Если события образуют пуассоновский поток, то число X событий, попадающих на любой участок времени (t₀, t₀ + t), распределено по закону Пуассона:

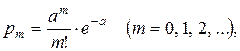
где a – математическое ожидание числа событий, попадающих на участок:

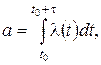
где l(t) – интенсивность потока.

Если l = const, то пуассоновский поток называется стационарным пуассоновским или простейшим. Для простейшего потока число событий, попадающих на любой участок времени длины t, распределено по закону Пуассона с параметром а = l × t.

В качестве примеров потоков можно рассматривать поступления вызовов на АТС, на пункт неотложной медицинской помощи, прибытие самолетов в аэропорт, клиентов на предприятие бытового обслуживания, последовательность отказов элементов некоторого устройства.