Функция распределения

Наиболее общей формой закона распределения СВ является функция распределения вероятностей.

Функцией распределения F(x) случайной величины X называется функция действительного аргумента x, значение которой для любого x равно вероятности события (X < x).

F(x) = P(X < x). (1.6)

Функция распределения обладает следующими свойствами:

1) 0 ≤ F(x) ≤ 1, – ¥ < x < ¥;

2)

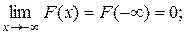
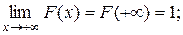
3) F(x) – неубывающая функция на всей числовой оси;

4) F(x) – непрерывна слева, т. е.

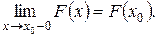
Вероятность попадания случайной величины на произвольный промежуток действительной оси [x₁; x₂) определяется формулой

P(x₁ ≤ X < x₂) = F(x₂) – F(x₁). (1.7)

Для дискретной СВ X функция распределения F(x) представляет собой разрывную ступенчатую функцию, скачки которой соответствуют возможным значениям x₁, x₂, … случайной величины X и равны вероятностям p₁, p₂, … этих значений; между скачками функция F(x) сохраняет постоянное значение.

Для дискретных СВ X функция распределения F(x) задается формулой

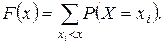(1.8)

На рисунке 2 схематически изображен график функции распределения дискретной случайной величины X, принимающей конечное множество значений {x₁, x₂, …, x_n}.

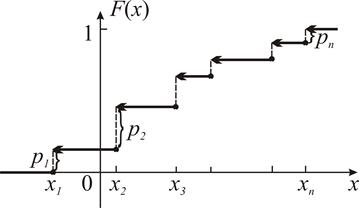
Рис. 2