Проверка некоторых равенств со множествами
В этом параграфе будет более подробно рассказано о том, как проверять равенства множеств. Хорошим наглядным средством для этого служат диаграммы Эйлера-Венна, на которых множества условно изображаются в виде геометрических фигур на плоскости (как правило, в виде кругов). Это даёт возможность наглядно представить себе процесс построения более сложных множеств из простых с помощью изученных в предыдущем параграфе основных операций над множествами.
Пример.Ниже представлены диаграммы Эйлера-Венна для множеств A È B, A Ç B, A \ B, B \ A, A Ç (B È C), (A Ç B) È (A Ç C):
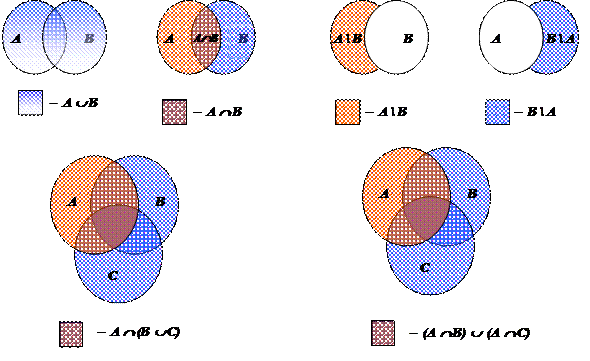
Эти диаграммы наводят на мысль, что последние два множества должны совпадать: A Ç (B È C) = (A Ç B) È (A Ç C). Однако такое зрительное восприятие не является доказательством равенства множеств, оно лишь может помочь заметить это равенство. Чтобы получить формальное доказательство равенства указанных множеств, нужно, следуя определению, доказать, что для любого x верно x Î A Ç (B È C) « x Î (A Ç B) È (A Ç C). Это можно сделать, следуя приводимому ниже общему алгоритму:
1.расписываем все отношения принадлежности в левой и правой частях доказываемой эквивалентности, следуя формальному определению операций над множествами:
x Î A Ç (B È C) º (x Î A) Ù (x Î B È C) º (x Î A) Ù (x Î B Ú x Î C),
x Î (A Ç B) È (A Ç C) º x Î (A Ç B) Ú x Î (A Ç C) º
º (x Î A Ù x Î B) Ú (x Î A Ù x Î C).
Таким образом, левая и правая части доказываемой эквивалентности записаны через элементарные высказывания вида x Î Y и их отрицания x Ï Y º º 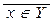 с помощью логических связок.
с помощью логических связок.
2.для участвующих в полученных записях элементарных высказываний введём буквенные обозначения: так, в рассматриваемом конкретном случае, обозначим a = (x Î A), b = (x Î B), c = (x Î C), сведя доказательство к проверке истинности формулы a Ù (b Ú c) « (a Ù b) Ú (a Ù c).
3.равенство множеств имеет место тогда и только тогда, когда полученная формула будет законом логики: в рассматриваемом случае это закон дистрибутивности. Следовательно, рассматриваемое равенство множеств A Ç (B È C) = (A Ç B) È (A Ç C) доказано.
В дальнейшем будут приведены другие примеры доказательств равенств множеств.
Если же на диаграммах Эйлера-Венна получаются заведомо разные рисунки множеств, то равенство множеств не выполнено, т.к. оно нарушается уже в частном случае фигур на плоскости. Например, A \ B ¹ B \ A, что видно из построенных выше диаграмм Эйлера-Венна для множеств A \ B и B \ A.
Теорема (об основных равенствах множеств). (I) Для любых множеств A, B, C справедливы следующие равенства:
(1) A = A (закон тождества),
(2) A Ç A = A (идемпотентность пересечения),
A È A = A (идемпотентность объединения),
(3) A Ç B = B Ç A (коммутативность пересечения ),
A È B = B È A (коммутативность объединения),
(4) (A Ç B) Ç C = A Ç (B Ç C) (ассоциативность пересечения),
(A È B) È C = A È (B È C) (ассоциативность объединения),
(5) (A È B) Ç C = (A Ç С) È (B Ç C) (законы дистрибутивности
(A Ç B) È C = (A È С) Ç (B È C) пересечения и объединения),
(6) A \ (B \ C) = (A \ B) È (A Ç C),
(7) (A \ B) \ C = (A \ C) \ B = A \ (B È C),
(8) A = (A Ç B) È (A \ B) и (A Ç B) Ç (A \ B) = Æ,
(9) A \ (B Ç C) = (A \ B) È (A \ C),
A \ (B È C) = (A \ B) Ç (A \ C),
(10) (A Ç B) \ C = (A \ C) Ç (B \ C),
(A È B) \ C = (A \ C) È (B \ C),
(11) A \ A = Æ, A È Æ = A, A Ç Æ = Æ.
(II) Если U – универсальное множество, то для любых множеств А и В справедливы равенства:
(12) A È U = U, A Ç U = A,
(13) A Ç 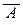 = Æ, A È
= Æ, A È 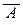 = U,
= U,
(14) 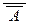 = A,
= A,
(15) 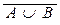 =
= 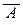 Ç
Ç 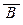 ,
, 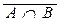 =
= 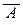 È
È 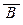
(16) A Í B тогда и только тогда, когда 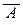 Ê
Ê 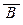 .
.
Доказательство. Докажем лишь некоторые равенства, оставляя остальные в качестве упражнений.
 (3) A Ç B = B Ç A. Вначале строим диаграмму Эйлера-Венна, которая подтверждает правдоподобность доказываемого равенства.
(3) A Ç B = B Ç A. Вначале строим диаграмму Эйлера-Венна, которая подтверждает правдоподобность доказываемого равенства.
Теперь докажем формально: нужно доказать, что x Î A Ç B « xÎ B Ç A. Имеем:
xÎ A Ç B º (x Î A) Ù (x Î B), xÎ B Ç A º (x Î B) Ù (x Î A),
и обозначая а = (x Î A), b = (x Î B), приходим к формуле a Ù b « b Ù a, которая является законом логики (закон коммутативности конъюнкции).
Равенство множеств A Ç B = B Ç A доказано.
(8) A = (A Ç B) È (A \ B), (A Ç B) Ç (A \ B) = Æ. Строим диаграмму Эйлера-Венна, которая подтверждает правдоподобность доказываемых равенств.
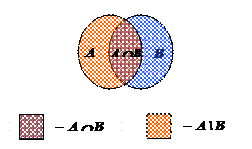 Теперь докажем первое равенство: нужно доказать, что x Î A « xÎ (A Ç B) È (A \ B).
Теперь докажем первое равенство: нужно доказать, что x Î A « xÎ (A Ç B) È (A \ B).
x Î (A Ç B) È (A \ B) º
º (x Î A Ç B)Ú (x Î A \ B) º
º (x Î A Ù x Î B) Ú (x Î A Ù 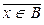 ).
).
Таким образом, обозначив a = (x Î A), b = (x Î B), получим формулу a « (a Ù b) Ú (a Ù 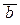 ), которая является законом логики: (a Ù b)Ú (a Ù
), которая является законом логики: (a Ù b)Ú (a Ù 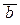 ) º a Ù (bÚ
) º a Ù (bÚ 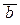 ) º a Ù 1 º a. Равенство множеств A = (A Ç B) È (A \ B) доказано.
) º a Ù 1 º a. Равенство множеств A = (A Ç B) È (A \ B) доказано.
Для доказательства второго равенства (A Ç B) Ç (A \ B) = Æ нужно лишь учесть, что по определению пустого множества, высказывание x Î Æ тождественно ложно. Таким образом, остаётся доказать, что x Î (A Ç B) Ç (A \ B) « 0. Это делается по стандартной схеме:
x Î (A Ç B) Ç (A \ B) º (x Î A Ç B) Ù (x Î A \ B) º
º (x Î A Ù x Î B) Ù (x Î A Ù x Ï B) º (a Ù b) Ù (a Ù 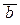 ) º a Ù b Ù a Ù
) º a Ù b Ù a Ù 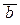 º
º
º a Ù a Ù b Ù 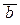 º a Ù 0 º 0.
º a Ù 0 º 0.
Утверждение (8) доказано.
(9) A \ (B È C) = (A \ B) Ç (A \ C). Строим диаграммы Эйлера-Венна, которые подтверждают правдоподобность доказываемого равенства.
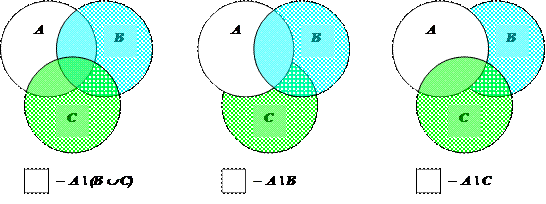
Формальное доказательство проводится стандартно: для проверки истинности формулы x Î A \ (B È C) « x Î (A \ B) Ç (A \ C) перепишем её левую и правую части, используя определения операций над множествами:
x Î A \ (B È C) º x Î A Ù 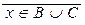 º x Î A Ù
º x Î A Ù 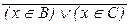 º a Ù
º a Ù  ,
,
x Î (A \ B) Ç (A \ C) º (x Î A \ B) Ù (x Î A \ C) º
º (x Î A Ù x Ï B) Ù (x Î A Ù x Ï C) º (a Ù 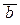 ) Ù (a Ù
) Ù (a Ù 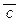 ).
).
Остаётся проверить, что формула a Ù  « (a Ù
« (a Ù 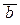 ) Ù (a Ù
) Ù (a Ù 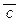 ) является законом логики. Это следует из законов ассоциативности, коммутативности, идемпотентности и законов де Моргана:
) является законом логики. Это следует из законов ассоциативности, коммутативности, идемпотентности и законов де Моргана:
a Ù  º a Ù (
º a Ù ( 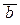 Ù
Ù 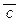 ) º a Ù a Ù
) º a Ù a Ù 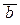 Ù
Ù 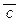 º (a Ù
º (a Ù 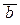 ) Ù (a Ù
) Ù (a Ù 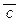 ).
).
Равенство A \ (B È C) = (A \ B) Ç (A \ C) доказано.
Все утверждения п. (II)теоремы можно вывести из уже доказанных равенств п. (I).
(12) A Ç U = A. В самом деле,
A = (A Ç U) È (A \ U) = (A Ç U) È Æ = A È U.
Здесь использовано равенство A \ U = Æ, которое легко следует из того, что А Í U: x Î A \ U º x Î A Ù x Ï U º x Î A Ù 0º 0 º x Î Æ.
(14) 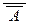 = A. Действительно,
= A. Действительно,
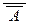 = U \
= U \ 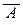 = U \ (U \ A) = (U \ U) È (U Ç A) = Æ È A = A.
= U \ (U \ A) = (U \ U) È (U Ç A) = Æ È A = A.
(16) Если A Í B, то x Î A ® x Î B – тождественно истинное высказывание. Докажем, что 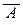 Ê
Ê 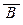 , т.е. что высказывание x Î
, т.е. что высказывание x Î 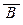 ® x Î
® x Î 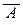 тоже тождественно истинно. Пусть, как обычно, a = (x Î A), b = (x Î B). Тогда x Î
тоже тождественно истинно. Пусть, как обычно, a = (x Î A), b = (x Î B). Тогда x Î 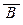 º x Ï B º
º x Ï B º 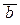 , x Î
, x Î 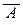 º
º  и по закону контрапозиции получаем x Î
и по закону контрапозиции получаем x Î 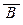 ® x Î
® x Î 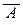 º (
º ( 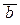 ®
®  ) « (a ® b) º 1, что и требовалось.
) « (a ® b) º 1, что и требовалось.
Если наоборот 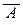 Ê
Ê 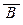 , то по уже доказанному,
, то по уже доказанному, 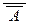 Í
Í 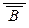 , т.е. A Í B, что и требовалось.
, т.е. A Í B, что и требовалось.
Теорема доказана.
Дата добавления: 2021-12-14; просмотров: 697;











