Универсальные множества и операция дополнения

В некоторых случаях все множества, участвующие в математических рассуждениях, содержатся в одном множестве U, которое называется универсальным множеством или универсумом.

Например, в школьной планиметрии рассматривались точки, прямые и фигуры, являющиеся подмножествами фиксированной плоскости, которую и можно считать универсальным множеством. Специалист по математическому анализу, как правило, работает в пространстве Rⁿ, которое для него является универсумом.

Если U – универсальное множество, то все объекты и множества их содержатся в U, так что высказывания x Î U, а также A Í U для любых элементов x и множеств A являются тождественно истинными, а высказывания x Ï U и A 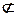U – тождественно ложными.

При наличии универсального множества определена ещё одна операция над множествами:

VI. Если U – универсальное множество, А Í U, то дополнением множества А называется множество 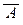= U \ А.

Ясно, что операция дополнения является частным случаем операции разности множеств. При этом x Î 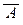º x Î U \ А º x Î U Ù x Ï A º 1 Ù x Ï A º x Ï A.

Примеры: 1. Пусть U = R, A = (–5; 2] È (3; +∞).Изобразим на числовой оси множество 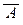= (–∞; –5] È (2; 3]:

2. В коробке лежат шары: 10 красных, 8 белых и 5 чёрных. Какое наименьшее количество шаров нужно вытащить из коробки, чтобы среди них наверняка оказалось 3 красных ?

Пусть U – множество всех шаров в коробке, А – множество красных шаров. Тогда 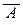– множество остальных (белых или чёрных) шаров, и количество элементов в 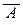равно 13 (= 8+5). Каждый вытащенный из коробки шар принадлежит либо множеству А, либо множеству 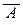, поэтому, вытащив первые 13 шаров нельзя быть уверенным, что среди них есть хотя бы один красный. Зато, вытащив ещё 3 шара, можно наверняка утверждать, что среди этих 16-ти шаров 3 окажутся красными. Таким образом, нужно вытащить 16 шаров.

Упражнения: 1. Почему в предыдущем примере недостаточно вытащить 15 шаров ?

2.Какое наименьшее количество шаров (в условиях примера 2) нужно вытащить из коробки, чтобы среди них наверняка оказалось 3 красных и один белый ?