Функции и их основные виды

Пусть A и B – два непустых множества. Если бинарное отношение Æ ¹ f Í A´B удовлетворяет следующему условию функциональности: " a Î D(f) $ ! b Î B a f b , то оно называется функцией из А в В. Для функций обычно вместо записи a f b пишут b = f(a) и элемент b Î B называют значением функции f в точке a Î A. Кроме того, тот факт, что бинарное отношение f Í A´B является функцией из A в B кратко записывают так: f: A ® B.

Примеры: 1. Пусть A = B = R, f = {(a; b) Î R´R | b = |a|}. Тогда f – функция: для любого a Î D(f) = Rзначение b определено однозначно, т.к. b = |a|. На самом деле f – это знакомая со школы функция модуля: " x Î R f(x) = |x|. При этом Im(f) = R₊₀ = {r Î R | r ³ 0}.

2. В отличие от предыдущего примера при A = B = R бинарное отношение f = {(a; b) Î R´R | a = |b|} функцией не является,т.к. например, при a = 1 обе пары (1; 1) и (1; –1) принадлежат f.

3. Пусть A = R, B = [–1; 1], f = {(a; b) Î A´B | b = sin a} – обычная функция синус с областями определения D(f) = Rи значений Im(f) = [–1; 1].

4. В отличие от предыдущего примера при A = R, B = [0; 1] множество f = {(a; b) Î A´B | b = sin a}, хотя и является функцией f : A ® B, но она отличается от функции синуса:

D(f) = {a Î R | 0 £ sin a £ 1} = È [0+2×p×n; 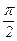+ 2×p×n], (n Î Z).

Это показывает, что нужно чётко определить понятие равенства функций.

Две функций f : A ® B и g : C ® D называются равными, если одновременно выполнены следующие условия:

A = C, B = D, D(f) = D(g) , " x Î D(f) f(x) = g(x).

Примеры: 1.Две функции f : R ® R, g : R ® R₊, заданные одной формулой " x Î R f(x) = e^x = g(x) различны, т.к. в обозначениях определения равенства A = C, но B ¹ D.

2. Две функции f : R₊ ® R , где " x Î R₊ f(x) = x, и g: R₊ ® R , где " x Î R₊ g(x) = e ^lnx, равны между собой, т.к. при x > 0 e^{ln x} = x.

3. Две функции f : R ® R , где " x Î R f(x) = x, и g: R ® R , где g(x) = e ^lnx, не равны между собой, т.к. D(f) = R ¹ R₊ = D(g).

Упражнения: 1. Будут ли функциями множества

а) f = {(x; y) Î R´R | y = ln x+ln(–x)}, б)f = {(x; y) Î R´R | y = ln x+ln|x|},

в)f = {(x; y) Î R´R | x+y = |x|+|y|}, г)f = {(x; y) Î R₊´R₊ | x+y = |x|+|y|},

д)f = {(x; y) Î R´R₊ | x+y = |x|+|y|} ?

2. Найдите области определения и значений функций

а) f = {(x; y) Î R´R | y = ln(–x)}, б) f = {(x; y) Î R´R | y = e^x+ln x },

в) f = {(x; y) Î R₊´R₊ | x+y = |x|+|y|}, г) f = {(x; y) Î R₊´R₊ | y = x+|y|},

д) f = {(x; y) Î R´[0; 1] | y = cos x + sin x}.

3. Равны ли следующие функции:

а) f : R ® R, f(x) = sin x и g : R ® [–1; 1], g(x) = sin x,

б) f : R ® R, f(x) = x и g : R ® R, g(x) = e ^{ln x},

в) f : R ® {0}, f(x) = 0 и g : R ® {0}, g(x) = cos(arc cos x),

г) f : R ® R, f(x) = 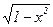и g : R ® R, g(x) = cos(arc sin x) ?

Графики функций

График функции f : A ® B – это график соответствующего ей бинарного отношения Æ ¹ f Í A´B. Таким образом, Г(f) = {(a; b) Î A´B | a f b} формально совпадает с самим множеством f, хотя и изображается на плоскости R´R. В этом отличие введённого понятия функции от школьного определения, в котором график функции – кривая на плоскости, а сама функция – закон соответствия y = f(x).

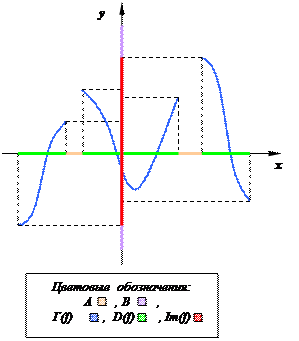Условие функциональности " a Î D(f) $ ! b Î B b = f(a) означает, что каждая вертикальная прямая y = x₀ Î A пересекает график функции не более, чем в одной точке. При этом области

D(A) = {a Î A | $ b Î B b = f(a)},

Im(f) = {b Î B | $ a Î A b = f(a)}

определения и значений функции будут изображаться ортогональными проекциями графика функции f на оси Ox и Oy соответственно.

Упражнения: 1. Постройте графики функций:

а) y = sin(0,5×x – p / 2), б)y = 1/(x² – 1), в) f = {(a; b) Î R´R | e ^a+b = 1},

г) y = 2^x+2^–x.

2. Найдите области определения и значений функций из упражнения 1.

3. Найдите все функции f : [0; 1] ® [0; 1] с условиями D(f) = [0; 1] = = Im(f), графики которых одновременно симметричны относительно двух прямых y = x, y = 1 – x.