Отношения эквивалентности и разбиения множеств
Бинарное отношение r на множестве А называется отношением эквивалентности, если оно является рефлексивным, симметричным и транзитивным.
Примеры: 1. Отношение равносильности º является отношением эквивалентности на множестве Ф всех формул исчисления высказываний.
2. Отношение равенства = множеств является отношением эквивалентности на множестве B(U) – множестве всех подмножеств множества U.
 3. Отношением эквивалентности будет бинарное отношение подобия ~ треугольников на множестве D всех треугольников плоскости.
3. Отношением эквивалентности будет бинарное отношение подобия ~ треугольников на множестве D всех треугольников плоскости.
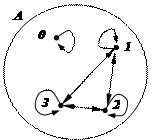
4. Будет отношением эквивалентности и бинарное отношение r на множестве А = {0, 1, 2, 3}, заданное графом, приведённым слева.
5. Пусть A = Z , x r y Û (x – y M 3). Проверим, будет ли r отношением эквивалентности ?
Рефлексивность: " a Î Z a – a M 3 – верно, т.к. 0 M 3. Значит, r рефлексивно.
Симметричность: " a, b Î R a – b M 3 « b – a M 3 – верно, т.к. если a – b M 3, т.е. a – b = 3×q (q Î Z), то b – a = 3×(–q), т.е. b – a M 3.Значит, r симметрично.
Транзитивность: " a, b, c Î Z a – b M 3 Ù b – c M 3 ® a – c M 3. Это тоже верно: если a – b M 3 и b – c M 3, то a – c = (a – b)+(b – c) M 3. Таким образом, r транзитивно.
Итак, r – отношение эквивалентности.
Для отношения эквивалентности r на множестве A с каждым элементом a Î A можно связать множество  = {b Î A | a r b}, которое называется классом эквивалентности отношения r с представителем a. Множество
= {b Î A | a r b}, которое называется классом эквивалентности отношения r с представителем a. Множество 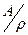 = {
= {  | a Î A} всех классов эквивалентности отношения r называется фактор-множеством множества A по отношению эквивалентности r.
| a Î A} всех классов эквивалентности отношения r называется фактор-множеством множества A по отношению эквивалентности r.
Примеры: 1. Найдём все классы эквивалентности и фактор-множество для отношения эквивалентности из предыдущего примера 4.
Ясно, что 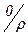 = {b Î A | 0 r b} = {0},
= {b Î A | 0 r b} = {0}, 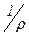 = {b Î A | 1 r b} = {1, 2, 3},
= {b Î A | 1 r b} = {1, 2, 3}, 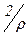 = {b Î A | 2 r b} = {1, 2, 3},
= {b Î A | 2 r b} = {1, 2, 3}, 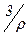 = {b Î A | 3 r b} = {1, 2, 3}. Таким образом, получилось всего два различных класса эквивалентности:
= {b Î A | 3 r b} = {1, 2, 3}. Таким образом, получилось всего два различных класса эквивалентности: 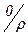 = {0} и
= {0} и 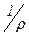 =
= 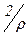 =
= 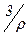 = {1, 2, 3}, т.е. фактор-множество
= {1, 2, 3}, т.е. фактор-множество 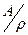 = {
= { 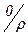 ,
, 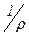 } в данном случае состоит из двух элементов. При этом множество А = {0, 1, 2, 3} разбилось на два непересекающихся подмножества: А = {0} È {1, 2, 3}, которые и являются найденными классами эквивалентности:
} в данном случае состоит из двух элементов. При этом множество А = {0, 1, 2, 3} разбилось на два непересекающихся подмножества: А = {0} È {1, 2, 3}, которые и являются найденными классами эквивалентности:
| А | |
| 1, 2, 3 |
2. Найдём все классы эквивалентности и фактор-множество для отношения эквивалентности из предыдущего примера 5.
Имеем:
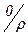 = {b Î Z | 0 r b} = {b Î Z | 0 – b M 3} = {b Î Z | b M 3} =
= {b Î Z | 0 r b} = {b Î Z | 0 – b M 3} = {b Î Z | b M 3} =
= {… , –6, –3, 0, 3, 6, …},
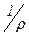 = {b Î Z | 1 r b} = {b Î Z | 1 – b M 3} = {b Î Z | 1 – b = 3×q (q Î Z)} = = {b Î Z | b = 3×q – 1} = {… , –7, –4, –1, 2, 5, 8, …},
= {b Î Z | 1 r b} = {b Î Z | 1 – b M 3} = {b Î Z | 1 – b = 3×q (q Î Z)} = = {b Î Z | b = 3×q – 1} = {… , –7, –4, –1, 2, 5, 8, …},
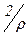 = {b Î Z | 2 r b} = {b Î Z | 2 – b M 3} = {b Î Z | 2 – b = 3×q (q Î Z)} = = {b Î Z | b = 3×q – 2} = {… , –8, –5, –2, 1, 4, 7, …}.
= {b Î Z | 2 r b} = {b Î Z | 2 – b M 3} = {b Î Z | 2 – b = 3×q (q Î Z)} = = {b Î Z | b = 3×q – 2} = {… , –8, –5, –2, 1, 4, 7, …}.
Дальнейшие попытки не дают новых множеств: например,
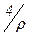 = {b Î Z | 4 r b} = {b Î Z | 4 – b M 3} = {b Î Z | 4 – b = 3×q (q Î Z)} = = {b Î Z | b = 3×q – 4} = {… –7, –4, –1, 2, 5, 8 …} =
= {b Î Z | 4 r b} = {b Î Z | 4 – b M 3} = {b Î Z | 4 – b = 3×q (q Î Z)} = = {b Î Z | b = 3×q – 4} = {… –7, –4, –1, 2, 5, 8 …} = 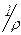 .
.
Докажем, что полученные три класса эквивалентности и составляют фактор-множество 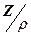 (т.е. что других классов уже нет). Это легко сделать, если вспомнить, что при делении на 3 любое целое число даёт остаток, равный либо 0, либо 1, либо 2. Найденные три класса эквивалентностей как раз и состоят из чисел, дающих при делении на 3 остатки 0 – класс
(т.е. что других классов уже нет). Это легко сделать, если вспомнить, что при делении на 3 любое целое число даёт остаток, равный либо 0, либо 1, либо 2. Найденные три класса эквивалентностей как раз и состоят из чисел, дающих при делении на 3 остатки 0 – класс 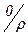 , 1 – класс
, 1 – класс 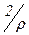 и 2 – класс
и 2 – класс 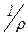 . Если взять любое число x Î Z, то оно попадёт в один из найденных классов, пусть, например, x Î
. Если взять любое число x Î Z, то оно попадёт в один из найденных классов, пусть, например, x Î 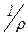 (т.е. что x = 2 + 3×n, n Î Z) и докажем, что
(т.е. что x = 2 + 3×n, n Î Z) и докажем, что 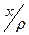 =
= 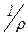 . Действительно, y Î
. Действительно, y Î 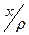 Û y Î {b Î Z | x r b} = = {b Î Z | x – b M 3} Û x – y = 3×q (q Î Z) Û y = x – 3×q = 2 + 3×n – 3×q = = 2 + 3×(n – q) Û (y даёт остаток 2 при делении на 3) Û y Î
Û y Î {b Î Z | x r b} = = {b Î Z | x – b M 3} Û x – y = 3×q (q Î Z) Û y = x – 3×q = 2 + 3×n – 3×q = = 2 + 3×(n – q) Û (y даёт остаток 2 при делении на 3) Û y Î 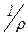 .
.
Итак, 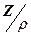 = {
= { 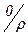 ,
, 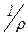 ,
, 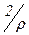 }, и само множество всех целых чисел Z разбивается на три непересекающиеся части, являющиеся найденными классами эквивалентности:
}, и само множество всех целых чисел Z разбивается на три непересекающиеся части, являющиеся найденными классами эквивалентности:
| Z | … , –6, –3, 0, 3, 6, … |
| … , –8, –5, –2, 1, 4, 7, … | |
| … , –7, –4, –1, 2, 5, 8, … |
Сделанные наблюдения можно обобщить:
Лемма (о классах эквивалентности).Пусть r – отношение эквивалентности на множестве А. Тогда
(1) " a Î A  ¹ Æ,
¹ Æ,
(2) " a, b Î A (  =
= 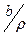 ) « a r b,
) « a r b,
(3) " a, b Î A (  ¹
¹ 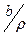 ) « (
) « (  Ç
Ç 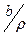 = Æ ) ,
= Æ ) ,
(4) " a Î A $ b Î A a Î 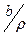 , т.е. A = È {
, т.е. A = È { 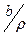 | b Î A}.
| b Î A}.
Доказательство. (1) По свойству рефлексивности отношения эквивалентности r имеем " a Î A a r a, т.е. a Î {b Î A | a r b} =  , т.е.
, т.е.  ¹ Æ.
¹ Æ.
(2) (Þ) Если  =
= 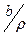 , то b Î
, то b Î 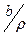 =
=  = {b Î A | a r b}, так что a r b.
= {b Î A | a r b}, так что a r b.
(Ü) Предположим, что a r b и докажем равенство  =
= 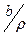 , проверив два включения
, проверив два включения  Í
Í 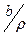 и
и  Ê
Ê 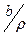 .
.
Если x Î  = {y Î A | a r y}, то a r x, и учитывая, что a r b, получим a r x Ù a r b º {симметричность r} º x r a Ù a r b, откуда по транзитивности отношения r заключаем x r b º b r x, т.е. x Î
= {y Î A | a r y}, то a r x, и учитывая, что a r b, получим a r x Ù a r b º {симметричность r} º x r a Ù a r b, откуда по транзитивности отношения r заключаем x r b º b r x, т.е. x Î 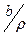 = {z Î A | b r z}. Таким образом,
= {z Î A | b r z}. Таким образом,  Í
Í 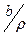 .
.
Если x Î 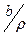 = {z Î A | b r z}, то b r x, и учитывая, что a r b, получим a r b Ù b r x, откуда по транзитивности отношения r заключаем a r x , т.е.
= {z Î A | b r z}, то b r x, и учитывая, что a r b, получим a r b Ù b r x, откуда по транзитивности отношения r заключаем a r x , т.е.
x Î  = {y Î A | a r x}, т.е.
= {y Î A | a r x}, т.е.  Ê
Ê 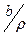 .
.
(3) (Þ) Если 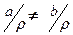 , но с Î
, но с Î 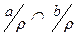 , то a r c Ù b r c º a r c Ù c r b, откуда по транзитивности, a r b и (ввиду (2))
, то a r c Ù b r c º a r c Ù c r b, откуда по транзитивности, a r b и (ввиду (2))  =
= 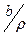 – противоречие.
– противоречие.
(Ü) Если 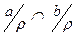 = Æ, то
= Æ, то 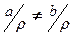 , ибо
, ибо 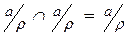 ¹ Æ – противоречие.
¹ Æ – противоречие.
(4) Если a Î A, то a Î  , так что можно взять b = a.
, так что можно взять b = a.
Лемма доказана.
Таким образом, фактор-множество 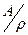 состоит из непустых подмножеств множества А (классов эквивалентности
состоит из непустых подмножеств множества А (классов эквивалентности  ), различные из которых не пересекаются, а в совокупности покрывают всё множество А (A = È {
), различные из которых не пересекаются, а в совокупности покрывают всё множество А (A = È {  | a Î A}), т.е.
| a Î A}), т.е. 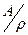 является разбиением множества А в смысле следующего определения.
является разбиением множества А в смысле следующего определения.
Пусть А – непустое множество. Разбиением множества А называется любое множество Xего подмножеств (X Í B(A)), удовлетворяющее следующим трём условиям:
(Р1): " x Î X x ¹ Æ (разбиение состоит из непустых множеств),
(Р2): " x, y Î X (x = y) Ú (x Ç y = Æ) (различные элементы разбиения не пересекаются),
(Р3): A = È X, т.е. " a Î A $ x Î X a Î x (разбиение покрывает всё множество А).
Теорема (о разбиении на классы эквивалентности). Пусть А – непустое множество. Тогда
(1) всякое отношение эквивалентности r на А определяет разбиение 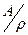 множества А на классы эквивалентности,
множества А на классы эквивалентности,
(2) Если X – разбиение множества А, то существует такое отношение эквивалентности r на А, что X = 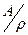 .
.
Доказательство. (1) уже доказано в лемме о классах эквивалентности.
(2) Пусть задано разбиение X множества А. Определим на А бинарное отношение r следующим образом: arb Û $ x Î X a Î x Ù b Î x (a, b Î A) и проверим, что r – искомое отношение эквивалентности.
Во-первых, r – действительно отношение эквивалентности:
Рефлексивность: (" a Î A a r a) º (" a Î A $ x Î X a Î x Ù a Î x) º º (" a Î A $ x Î X a Î x) – истинно ввиду (Р3).
Симметричность: (" a, b Î A a r b « b r a) º (" a, b Î A ($ x Î X a Î x Ù Ù b Î x) « ($ x Î X b Î x Ù a Î x)) – очевидно выполнено.
Транзитивность: (" a, b, c Î A a r b Ù b r c ® a r c) º (" a, b, c Î A ($ x Î X a Î x Ù b Î x) Ù ($ y Î X b Î y Ù c Î y) ® ($ z Î X a Î z Ù c Î z). Поскольку b Î x Ç y, то x Ç y ¹ Æ и по свойству (Р2), x = y. Таким образом, a Î x, b Î x, c Î x и можно взять z = x Î X .
Итак, r – отношение эквивалентности, удовлетворяющее условию " b Î A $ ! x Î X b Î x (доказано при обосновании транзитивности). В дальнейшем однозначно определённый элемент x Î Xсо свойством b Î x будем обозначать через x(b).Тогда определение бинарного отношения r можно записать в виде a r b Û x(a) = x(b) (a, b Î A).
Проверим, что X = 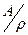 . Действительно, если x Î X, то по свойству (Р1) существует a Î x. Поэтому x = {b Î A | b Î x} = {b Î A | a Î x Ù b Î x} = = {b Î A | x(a) = x(b)} =
. Действительно, если x Î X, то по свойству (Р1) существует a Î x. Поэтому x = {b Î A | b Î x} = {b Î A | a Î x Ù b Î x} = = {b Î A | x(a) = x(b)} = 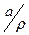 . Таким образом, X Í
. Таким образом, X Í 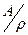 . Обратно, если a Î A, то
. Обратно, если a Î A, то 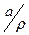 = {b Î A | a r b} = {b Î A | x(a) = x(b)} = x(a) Î X , т.е. X Ê
= {b Î A | a r b} = {b Î A | x(a) = x(b)} = x(a) Î X , т.е. X Ê 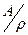 .
.
Теорема доказана.
Примеры: 1. Задать на множестве A = {0, 1, 3, 5} отношение эквивалентности с фактор-множеством 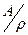 = {{1}, {3}, {0, 5}}.
= {{1}, {3}, {0, 5}}.
Во-первых, ясно, что задано разбиение множества A:
| А | |
| 0, 5 |
Исходя из построения отношения эквивалентности при доказательстве теоремы, можно выписать определение искомого отношения r : a r b Û $ x Î X a Î x Ù b Î x. Более конкретно для каждого элемента:
0 r b Û $ x Î X 0 Î x Ù b Î x Û b Î x = {0, 5},
1 r b Û $ x Î X 1 Î x Ù b Î x Û b Î x = {1},
3 r b Û $ x Î X 3 Î x Ù b Î x Û b Î x = {3},
5 r b Û $ x Î X 5 Î x Ù b Î x Û b Î x = {0, 5}.
Можно нарисовать граф полученного отношения эквивалентности:
 2. Пусть задано разбиение множества Zна два подмножества: чётных и нечётных чисел. Задать соответствующее отношение эквивалентности на множестве Z.
2. Пусть задано разбиение множества Zна два подмножества: чётных и нечётных чисел. Задать соответствующее отношение эквивалентности на множестве Z.
Понятно, что задано действительно разбиение множества Z:
| Z | … , –5, –3, –1, 1, 3, 5, … |
| … , –4, –2, 0, 2, 4, … |
В соответствии с общими рассуждениями искомое отношение эквивалентности r должно объявить эквивалентными между собой все нечётные числа (из первого множества разбиения) и эквивалентными между собой все чётные числа (из второго множества разбиения). Задать такое отношение можно многими способами. Например, a r b Û a – b M 2 (a, b Î Z) – один из возможных способов (проверьте !!).
Дата добавления: 2021-12-14; просмотров: 595;











