Основные типы бинарных отношений

Пусть r – бинарное отношение на множестве А, т.е. Æ ¹ r Í A´A. Говорят, что r

рефлексивно, если	" a Î A a r a
симметрично, если	" a, b Î A a r b « b r a
транзитивно, если	" a, b, c Î A a r b Ù b r c ® a r c
антирефлексивно, если	" a Î A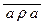
антисимметрично, если	" a, b Î A a r b Ù b r a ® a = b
функция, если	" a Î D(r) $ ! b Î B a r b

Легко понять, что означают эти свойства на языке графов и графиков:

Свойство	Граф	График
рефлексивность	в каждой вершине · а графа есть петля · a	график содержит диагональ D = {(a; a) Î A´A}:
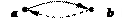
симметричность	у каждой стрелки в графе есть обратная (если есть a · ® · b, то должна быть и b · ® · a ):	график симметричен относительно диагонали:
транзитивность	… любой путь по стрелкам графа можно пройти по одному ребру:	? ? ?
анти- рефлексивность	в графе нет ни одной петли:	на графике нет ни одной точки диагонали:
анти- симметричность	в графе нет замкнутых путей длины два:	любые две симметричные относительно диагонали точки совпадают (и лежат на диагонали):
функция	из каждой вершины графа выходит не более одной стрелки:	любая вертикальная прямая x = a Î А пересекает график не более чем в одной точке:

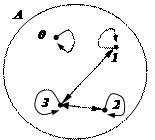Примеры: 1. Какими свойствами обладает бинарное отношение r со следующим графом ?

Ясно, что r рефлексивно, симметрично, не транзитивно: путь 1 · ® · 3 ® · 2 нельзя пройти по одной стрелке. Оно не антисимметрично и не антирефлексивно. Функцией не является, т.к. из вершин 1 · , 2 · , 3 · выходят более одной стрелки.

2. Какими свойствами обладает отношение r = {(1; 1), (2; 2)} Í N´N ?

Для удобства можно построить граф для r , который наглядно демонстрирует, что r не рефлексивно (например, нет петли у вершины 3 ·), симметрично, транзитивно, антисимметрично, но не антирефлексивно. При этом r является функцией.

3. Какими свойствами обладает бинарное отношение r, заданное правилом a r b Û |a – b| < 1 (a, b Î R) ?

Последовательно проверяем все свойства аналитически, т.к. построить граф в данном случае затруднительно.

Рефлексивность: (" a Î A a r a) Û (" a Î R |a – a| < 1) – верно, т.к. 0 < 1. Значит, r рефлексивно.

Симметричность: (" a, b Î A a r b « b r a) Û (" a, b Î R |a–b| < 1 « « |b – a| < 1) – верно.Значит, r симметрично.

Транзитивность: (" a, b, c Î A a r b Ù b r c ® a r c) Û (" a, b, c Î R |a – b| < 1 Ù |b – c| < 1 ® |a – c| < 1). Нетрудно понять, что это не верно: например, |0 – 0,5| < 1 Ù |0,5 – 1| < 1, но |0 – 1| = 1 ³ 1. Таким образом, r не транзитивно.

Антирефлексивность: (" a Î A 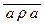) Û (" a Î R |a – a| ³ 1) – не верно, и r не антирефлексивно.

Антисимметричность: (" a, b Î A a r b Ù b r a ® a = b) Û (" a, b Î R |a – b| < 1 Ù |b – a| < 1 ® a = b) – не верно, т.к. |0 – 0,5| < 1 Ù |0,5 – 0| < 1, но 0,5 ¹ 0. Итак, r не антисимметрично.

Функциональность: (" a Î A " b, c Î B a r b Ù a r c ® b = c) Û (" a, b, c Î R |a – b| < 1 Ù |a – c| < 1 ® b = c) – не верно (?!). Значит, r – не функция.

Упражнения: 1. Обоснуйте свойства отношения r из примера 3, построив график этого отношения.

2. Какими свойствами обладают бинарные отношения r со следующими графиками:

3. Исследуйте свойства бинарных отношений:

a) r = {(1; 3), (3; 5), (5; 7), …} Í N´N, б) a r b Û a²= b² (a, b Î N),

в)a r b Û a² = b² (a, b Î R), г) r = {(x; y) Î N´N | |y – x| > 5}.