Основные операции над множествами

Основные понятия и операции

В фундаменте современных математических теорий лежат понятия множества, элемента множества, отношения принадлежности элемента множеству. Интуитивный смысл этих понятий ясен: под множеством понимают совокупность некоторых объектов (которые называются элементами данного множества), мыслимых как единое целое. Для обозначения того, что объект a является элементом множества А, пишут a Î А (а принадлежит А). Вместо отрицания 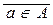используется запись а Ï А (а не принадлежит А).

Наиболее употребительны следующие два способа задания множеств:

· перечисление элементов (используется в основном для множеств, состоящих из конечного числа элементов). Например, запись А = {1, 2, –5, 3} означает, чтомножество А состоит из элементов 1, 2, –5, 3. Элементами множеств могут быть и объекты различной природы. Так, множество А = {1, {1}, a} состоит из числа 1, одноэлементного множества {1} (содержащего единственный элемент – число 1) и буквы а.

· выделение множества в другом множестве с помощью характеристического свойства его элементов: если В – множество и P(x) – некоторое свойство (высказывание о произвольном элементе x Î B), то можно определить новое множество А всех элементов x множества В, удовлетворяющих свойству P, написав А = {x Î B | P(x) (= 1)}. Так, например, R₊ = {x Î R | x > 0} – множество всех положительных действительных чисел.

Замечание: одно и то же множество можно задать различными способами: например, {r Î R | r² = 1} = {–1, 1} = {n Î Z | |n| = 1}. Поэтому важно ввести понятие равенства двух множеств.

Два множества А и В называются равными (символически А = В), если они состоят из одних и тех же элементов. Это значит, что для любого элемента а Î А выполнено а Î В, и для любого элемента b Î B выполняется b Î A. В противном случае множества А и В называются неравными: А ¹ В.

Множество А называют подмножеством множества В (говорят также, что А содержится в В или В содержит А) и записывают А Í В, если любой элемент множества А принадлежит множеству В.

Полезно ввести в рассмотрение пустое множество Æ = {x Î A | x Ï A}, не имеющее ни одного элемента. Ясно, что для любого множества A верно Æ Í A.

Примеры: 1. {1, 2, 3} = {3, 1, 2}. Хотя порядки перечисления элементов этих множеств и различны, но каждый элемент одного множества является элементом другого множества, что и обеспечивает их равенство.

2. {1, 2, 3} = {1, 1, 2, 3, 2, 1, 3}. Второе множество, хотя и выглядит толще первого, но на самом деле состоит их тех же элементов.

3. {1, 2, 3} ¹ {3, {1}, 2}. Элемент 1 первого множества не является элементом второго множества. Точно так же Элемент {1} второго множества не является элементом первого множества. Кстати, почему 1 ¹ {1} ?

4. А = {1, 2} ¹ {1, 2, –1} = В, т.к. –1 Î В, но –1 Ï А,но {1, 2} Í {1, 2, –1}, т.к. 1 Î В и 2 Î В.

5. Справедливы включения N = {1, 2, 3, …} Í Z = {… , –2, –1, 0, 1, 2, …} Í Í Q = { 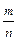Î R | m Î Z Ù n Î N} Í R .

Основные операции над множествами

I. Если А, В – множества, то существует множество А È В – объединение множеств А и В, которое состоит из всех элементов, являющихся элементами либо множества А, либо множества В:

x Î A È B « x Î A Ú x Î B.

Примеры: 1.Если A = {1, 2, 5, Æ}, B = {{1}, 2, 5, Æ}, то

А È В = {1, 2, 5, Æ, {1}}.

2. Если A = {x Î R | 1 < x £ 5}, B = {x Î R | –1 £ x < 2}, то

A È B = [–1; 5] = {x Î R | –1 £ x £ 5}.

II. Если А, В – множества, то существует множество А Ç В – пересечение множеств А и В, которое состоит из всех элементов, являющихся одновременно элементами и множества А, и множества В:

x Î A Ç B « x Î A Ù x Î B.

Примеры: 1. Если A = {1, 2, 5, Æ}, B = {{1}, 2, 5, Æ}, то

А Ç В = {2, 5, Æ}.

2. Если A = {x Î R | 1 < x £ 5}, B = {x Î R | –1 £ x < 2}, то

A Ç B = (1; 2) = {x Î R | 1 < x < 2}.

3. A Ç B = {a Î A | a Î B}.

На основе понятий пересечения и объединения двух множеств можно ввести аналогичные операции над несколькими множествами:

A₁ Ç … Ç A_n = (…((A₁ Ç A₂) Ç A₃) Ç …) Ç A_n ,

A₁ È … È A_n = (…((A₁ È A₂) È A₃) È …) È A_n .

III. Если А, В – множества, то существует множество А \ В – разность множеств А и В, которое состоит из всех элементов, принадлежащих множеству А, но не принадлежащих множеству В:

x Î A \ B « x Î A Ù x Ï B.

Примеры: 1. Если A = {1, 2, 5, Æ}, B = {{1}, 2, 5, Æ}, то А \ В = {1}.

2. Если A = (1; 5] = {x Î R | 1 < x £ 5}, B = [–1; 2) = {x Î R | –1 £ x < 2}, то A \ B = [2; 5].

3. A \ B = {a Î A | a Ï B}.

IV. Если А – множество, то существует множество всех его подмножеств B(A), называемое также булеаном множества А, и состоящее из всех подмножеств множества А: X Î B(A) « X Í A.

Важно отметить, что булеан B(A) состоит из множеств (подмножество множества А само является множеством) и содержит в качестве элементов пустое множество Æ и само множество А (которые в случае А = Æ совпадают).

Примеры: 1. Если А = Æ, то B(A) = {Æ}.

2.Если A = {1}, то B(А) = {Æ, {1}}.

3. Если A = {1, 2}, то B(А) = {Æ, {1}, {2}, {1, 2}}.

4. Если A = {1, 2, 3}, то

B(А) = {Æ, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}.

5.Можно доказать, что булеан n-элементного множества А состоит из 2ⁿ элементов. Поэтому булеан часто называют степенью множества А и обозначают 2^A.

V. Если А, В – множества, то существует их прямое (декартово) произведение А´В, состоящее из всех упорядоченных пар (a; b), где а Î А, b Î B:

А´В = {(a; b) | a Î A Ù b Î B}.

Примеры: 1.Если А = {1}, B = {0, 5}, то А´В = {(1; 0), (1; 5)}.

2. Если А = {0, 2}, B = {0, 5}, то А´В = {(0; 0), (0; 5), (2; 0), (2; 5)}.

3. Если множество А состоит из m элементов, а множество В – из n элементов, то можно доказать, что множество А´В состоит из m´n элементов. По этой причине в названии множества А´В используется термин “произведение”. Если А = B, то множество А´А состоит из m² элементов и называется декартовым квадратом множества А и обозначается через A².

Вслед за декартовым произведением двух можно ввести и декартово произведение A₁ ´ … ´ A_n = ( … ((A₁ ´ A₂) ´ A₃)´ …)´ A_n n множеств A₁ , … , A_n . Множество 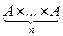называется декартовой степенью множества A и обозначается A ⁿ.

Декартово произведение А´В = {(a; b) | a Î A Ù b Î B} двух множеств А и В иногда условно изображают на плоскости, трактуя компоненты упорядоченной пары (a; b) как координаты: a – координата по оси x, на которой отмечают множество А, а b – координата по оси y, на которой отмечают множество В. Таким образом, элементы (a; b) Î А´B условноизображаютсяточками на плоскости с “координатами” a и b.

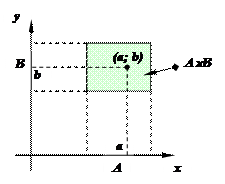Особенно удобно графическое изображение декартова произведения А´В в случае, когда А и В – числовые множества, т.е. А Í R, B Í R . Тогда изображение принимает не условный характер, а имеет вполне конкретный геометрический смысл: множество А´В представляет из себя множество точек M(a; b) декартовой плоскости, первая координата а которых принадлежит множеству А, а вторая b – принадлежит множеству В.

Пример.Изобразим множество А´В, где A = [1; 2], B = (2; 3).

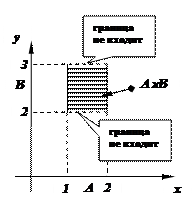
Понятие декартова (прямого произведения множеств) обобщается на случай произвольного количества множеств-сомножителей: если A₁ , … , A_k – множества, то их прямым (или декартовым) произведением А₁´ … ´А_k называют множество, состоящее из всех упорядоченных наборов (a₁ ; … ; а_k) длины k, где а_i Î А_i (1 £ i £ k):

А₁´ … ´ A_k = {(a₁ ; … ; a_k ) | a₁ Î A₁ Ù … Ù a_k Î A_k }.

Для k = 3 это множество можно аналогично случаю k = 2 условно изображать в пространстве. Если множества А_i содержат n_i элементов (1 £ i £ k), то их декартово произведение содержит n₁´ … ´n_k элементов. В случае A₁ = … = A_k = A декартово произведение А₁´ … ´ A_k называется k-й декартовой степенью множества А и обозначается через A^k. Это название обусловлено тем, что для n-элементного множества A декартова степень A^k содержит n^k элементов.

Упражнения: 1. Перечислите все элементы множеств A È B, A Ç B, A \ B, B(A), A´B для A = {Æ, 0, {1}}, B = {{Æ}, 0, 1}.

2.Изобразите на числовой оси следующие множества A È B, A Ç B, A \ B, B \ A, (A È B) \ (B Ç A), B \ (A È B) для

а) А = (1; 3], B = [2; 3); б) А = [–1; 2) È (3; 5], B = [0; 2,5] È [4; 6);

в) A = (–∞; 2), B = [–4; +∞); г) A = (–∞; 0], B = (–∞; 5).

3. Изобразите на декартовой плоскости следующие множества:

[–1; 1]´(0; 3], {–1; 1}´(0; 3], [–1; 1]´{0; 3}, {–1; 1}´{0; 3}.

4. Что можно сказать о множествах А и В, если

а) АÈ В = А Ç В, б) А \ В = В \ А , в) А´В = В´А, г) А´В = Æ ,

д) А \ (B Ç A) = A \ B , е) A´(A Ç B) = (A È B)´B ?