Способы задания бинарных отношений

I. перечисление элементов (конечного) бинарногог отношения r:

r = {(a₁ ; b₁), … , (a_n ; b_n)} Í A´B

Пример. Если А = {0, 3, 5}, B = {1, 2, 3}, то

r = {(0; 1), (0; 2), (3; 3), (3; 2)} Í A´B

является бинарным отношением между элементами множеств А и В c областью определения D(r) = {0, 3} (в этом множестве собраны все первые компоненты пар, участвующих в r) и областью значений Im(r) = {1, 2, 3} (в этом множестве собраны все вторые компоненты пар, участвующих в r).

II. выделение бинарного отношения r в множестве А´В с помощью характеристического свойства P(x, y):

r = {(a; b) Î A´B | P(a, b) = 1} или a r b Û P(a, b) = 1 (a Î A, b Î B)

Характеристическое свойство бинарного отношения r – это такой предикат, область истинности которого совпадает с r (т.е. P(a, b) = 1 тогда и только тогда, когда a r b).

Примеры: 1. Бинарное отношение предыдущего примера можно задать, например, так: r = {(a; b) Î A´B | (a < 5) Ù (a + b ¹ 3) Ù (a×b ¹ 3)} или a r b Û (a < 5) Ù (a + b ¹ 3) Ù (a×b ¹ 3) (a Î {0, 3, 5}, b Î {1, 2, 3}).

2. Одно и то же бинарное отношение можно задать с помощью нескольких характеристических свойств. Например, бинарное отношение предыдущего примера можно задать и так:

a r b Û (a = 0 Ù b = 1) Ú (a = 0 Ù b = 2) Ú (a = 3 Ù b = 2) Ú (a = 3 Ù b = 3)

(a Î {0, 3, 5}, bÎ {1, 2, 3}).

3. Точно так же можно, не задумываясь, выписать характеристическое свойство для любого бинарного отношения r = {(a₁ ; b₁), … , (a_n ; b_n )} Í A´B с конечным числом элементов:

a r b Û (a = a₁ Ù b = b₁) Ú … Ú (a = a_n Ù b = b_n) (a Î A, b Î B).

Здесь очевидно будем иметь D(r) = {a₁ , … , a_n }, Im(r) = {b₁ , … , b_n }.

4.Задание a r b Û a² + b² = –1 (a, b Î R) не определяет бинарного отношения, т.к. среди действительных чисел нет ни одной пары (a; b), удовлетворяющей указанному характеристическому свойству. Бинарное отношение обязательно непусто !!

5. Бинарное отношение r = {(a; b) Î R´R | a² + b² = 1} бесконечно. Для него D(r) = = [–1; 1] = Im(r).

6. Для бинарного отношения с заданием a r b Û a² = b² (a Î R, b Î Z) получаем D(r) = Z(а не R !), Im(r) = Z. Это отношение можно задать и так: a r b Û a = ±b (a Î R, b Î Z).

III. с помощью графа (в основном для конечных отношений):

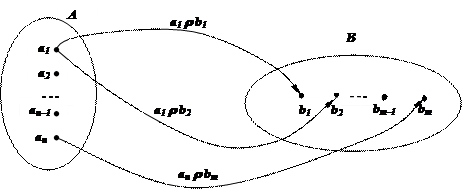
Неформально говоря, граф – это совокупность вершин, изображаемых точками, и рёбер или стрелок, соединяющих некоторые вершины. Для задания бинарного отношения r между элементами множеств A и B в качестве вершин берут множество всех элементов, принадлежащих A или В, т.е. множество A È B. При этом две вершины a Î A и b Î B соединяют стрелкой тогда и только тогда, когда a r b. Иногда для удобства стрелки подписываются, но делать это не обязательно: рисунок всё показывает сам.

Задание бинарного отношения в виде графа более наглядно, нежели формальные его задания. Оно позволяет сразу определить области определения и значения этого бинарного отношения: областью определения будет множество всех тех вершин a Î A, из которых выходит хотя бы одна стрелка, а областью значений – множество всех тех вершин b Î B, в которые входит хотя бы одна стрелка.

Примеры: 1. Для бинарного отношения из предыдущего примера 1 задание в виде графа будет выглядеть так:

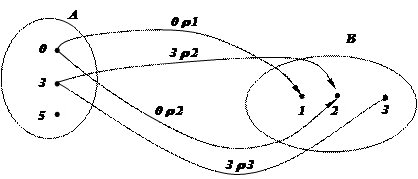Здесь видны множества А = {0, 3, 5}, B = {1, 2, 3}, D(r) = {0, 3}, Im(r) = В.

Замечание: необходимо на графе изображать все вершины, а не только те, в которые входят, или из которых выходят стрелки. Если в этом примере убрать вершину 5, то множество А изменится, и получится совсем другое бинарное отношение !

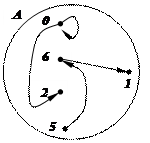2. Если бинарное отношение задано на множестве А, т.е. А = В, то не обязательно рисовать отдельно две копии вершин множества А, стрелками можно соединять вершины внутри множества А. Например, рисунок слева задаёт бинарное отношение на множестве А = {0, 1, 2, 5, 6} : r = {(0; 0), (0; 2), (5; 6), (6; 1)} Í А´А.

IV. с помощью графика на декартовой плоскости (в основном для числовых множеств А и В):

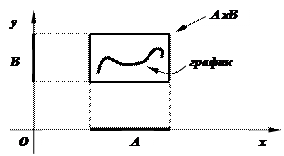При таком задании бинарного отношения множество А изображается (иногда условно) на оси Ox, а множество В – на оси Oy. Каждая пара (a; b), где a Î A, b Î B, изображается в виде точки на декартовой плоскости с координатами (a; b). Область (множество точек) в декартовом прямоугольнике А´В, образованная всеми точками с координатами (a; b), где a связано с b бинарным отношением r, называется графиком бинарного отношения r : Г(r) = {(a; b) Î A´B | a r b}.

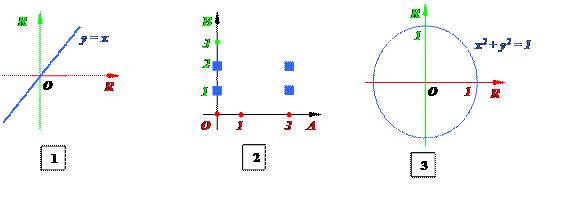
Примеры: 1. Бинарное отношение r = {(a; b) Î R´R | a = b} может быть задано графиком 1на рисунке ниже (прямая y = x).

2. График 2 определяет отношение r = {(0; 1), (0; 2), (3; 1), (3; 2)} Í A´B, где А = {0, 1, 3}, B = {1, 2, 3}.

3. График 3 определяет бинарное отношение, заданное характеристическим свойством a r b Û a² + b² = 1 (a Î R, b Î R).

Все описанные способы задания бинарных отношений эквивалентны: от любого из них можно перейти к каждому из остальных. Конечно, это не всегда просто сделать по техническим причинам (например, не всегда можно нарисовать хороший график или придумать компактное характеристическое свойство), но в принципе возможно.

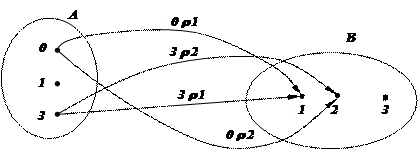Примеры: 1. Для бинарного отношения, заданного выше графиком 2, сразу выписывается задание с помощью перечисления: r = {(0;1),(0;2),(3;1),(3;2)} Í A´B, где А = {0, 1, 3}, B = {1, 2, 3}. По нему легко нарисовать граф (слева) и выписать характеристическое свойство: a r b Û (a – 1)×(b – 3) ¹ 0 (a Î {0, 1, 3}, b Î {1, 2, 3}).

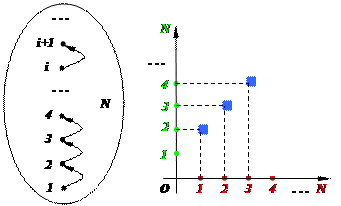2. Если бинарное отношение r задано следующим графом на множестве N, то можно сразу нарисовать его график, задать это бинарное отношение выделением r = {(x;y)Î N´N | y = x+1} и даже перечислить (несмотря на бесконечность r) r = {(1; 2), (2; 3), (3; 4), …}.

Упражнения: 1. Задайте всеми возможными способами:

a) r = {(1; 3), (3; 5), (5; 7), …} Í N´N,

б) a r b Û a £ b² (a, b Î N),

в) r = {(x; y) Î N´N | |y – x| £ 5}.

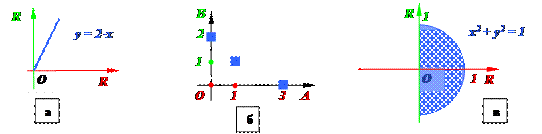2. Задайте всеми возможными способами бинарные отношения по их графикам:

3. Задайте всеми способами бинарные отношения по их графам:

<1 2 345 6 7 >

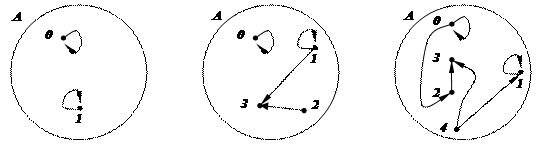Дата добавления: 2021-12-14; просмотров: 388;