И равносильные формулы
Примеры предыдущего параграфа показывают, что таблицы истинности формул могут быть разнообразны. Формулы, принимающие при любых наборах значений пропозициональных переменных одно и то же значение 0, называются противоречиямиили тождественно ложными. Формулы, принимающие при любых наборах значений пропозициональных переменных одно и то же значение 1, называются тавтологиями, законами логикиили тождественно истинными. Остальные формулы, которые принимают хотя бы одно значение 0 и хотя бы одно значение 1, называются выполнимыми. Для обозначения противоречия или закона логики A(x1 , … , xn) кратко будем писать A(x1 , … , xn) º 0 и A(x1 , … , xn) º 1соответственно.
Как следует из определений, для того, чтобы проверить к какому именно виду (закон логики, противоречие или выполнимая) относится данная формула, нужно построить её таблицу истинности и проанализировать последний столбец этой таблицы: если он состоит из одних единиц, то формула будет законом логики, если – из одних нулей, то – противоречием, а в противном случае – формула выполнима.
Пример: Определить вид формулы A = ( 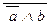 ® a) « (a Ú b).
® a) « (a Ú b).
Строим таблицу истинности:
| a | b | 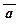
| 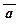 Ù b Ù b
| 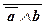
| 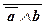 ® a ® a
| a Ú b | A |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
Таким образом, формула является законом логики: А º 1.
Теорема (об основных законах логики). Для любых формул A, B, C следующие формулы являются законами логики:
(1) A « A (закон тождества),
(2) (A Ù A) « A (идемпотентность конъюнкции),
(A Ú A) « A (идемпотентность дизъюнкции),
(3) (A Ù B) « (B Ù A) (коммутативность конъюнкции),
(A Ú B) « (B Ú A) (коммутативность дизъюнкции),
(4) ((A Ù B) Ù C) « (A Ù (B Ù C)) (ассоциативность конъюнкции),
((A Ú B) Ú C) « (A Ú (B Ú C)) (ассоциативность дизъюнкции),
(5) ((A Ú B) Ù C) « ((A Ù С) Ú (B Ù C)) (законы дистрибутивности
((A Ù B) Ú C) « ((A Ú С) Ù (B Ú C)) конъюнкции и дизъюнкции),
(6) 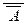 « A (закон двойного отрицания),
« A (закон двойного отрицания),
(7) 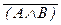 « (
« ( 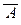 Ú
Ú 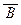 ) (законы
) (законы
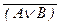 « (
« (  Ù
Ù 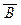 ) де Моргана),
) де Моргана),
(8) (A ® B) « ( 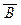 ®
®  ) (закон контрапозиции),
) (закон контрапозиции),
(9) (A « B) « ( 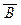 «
«  ) (закон противоположности),
) (закон противоположности),
(10) (A Ú (A Ù B)) « A (закон поглощения),
(11) (A Ù (A Ú B)) « A (закон ограничения),
(12) (A Ú (  Ù B)) « (A Ú B) (законы
Ù B)) « (A Ú B) (законы
(А Ù (  Ú B)) « (А Ù B) удаления),
Ú B)) « (А Ù B) удаления),
(13) (A Ù B) Ú (A Ù 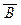 ) « A (законы склеивания
) « A (законы склеивания
(A Ú B) Ù (A Ú 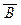 ) « A по В),
) « A по В),
(14) (A ® (B ® C)) « (B ® (A ® C)) (закон перестановки посылок),
(15) ((A ® B) Ù (B ® C)) ® (A ® C) (закон силлогизма),
(16) (A Ù B) ® A, (A Ù B) ® B (законы удаления конъюнкции),
(17) A ® (A Ú B), B ® (A Ú B) (законы введения дизъюнкции),
(18) ((  ® B) Ù (
® B) Ù ( 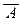 ®
® 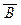 )) « A (закон обоснования от противного),
)) « A (закон обоснования от противного),
(19) (A Ú B) Ù (A ® C) Ù (B ® C) ® C (закон разбора случаев),
(20) ((A Ú B) Ù (C Ú 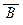 )) ® (A Ú C) (законы
)) ® (A Ú C) (законы
(B Ù (C Ú 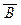 )) ® C резолюций),
)) ® C резолюций),
законы, выражающие одни логические связки через другие:
(21) (A ® B) « (  Ú B), (A ® B) «
Ú B), (A ® B) « 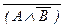 ,
,
(22) (A « B) « (A ® B) Ù (B ® A), (A « B) « 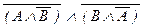 ,
,
(A « B) « 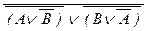 , (A « B) « (A Ù B) Ú (
, (A « B) « (A Ù B) Ú (  Ù
Ù 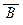 ),
),
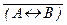 « (A Ù
« (A Ù 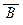 ) Ú (
) Ú (  Ù B),
Ù B),
(23) (A Ù B) « 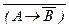 , (A Ù B) «
, (A Ù B) « 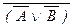 , A Ù
, A Ù 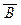 «
« 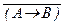 ,
,
(24) (A Ú B) « ( 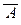 ® B), (A Ú B) «
® B), (A Ú B) « 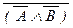 ,
,
законы действий с тавтологиями и противоречиями:
(25) (А Ù 1) « А, (A Ú 1) « 1,
(26) (А Ù 0) « 0, (A Ú 0) « A,
(27) (A Ù 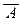 ) « 0, (A Ú
) « 0, (A Ú 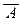 ) « 1,
) « 1,
(28) (A ® A) « 1, (0 ® A) « 1, (1 ® A) « A, (A ® 0) « 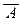 , (A ® 1) « 1,
, (A ® 1) « 1,
(29) (A « A) « 1, (A « 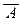 ) « 0, (A « 1) « A, (A « 0) «
) « 0, (A « 1) « A, (A « 0) « 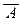 ,
,
(30) 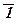 « 0,
« 0, 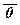 « 1.
« 1.
Доказательство. Упражняйтесь в построении таблиц истинности.
Замечание: Многочисленные законы логики, приведённые в этой теореме (так же как многочисленные основные равносильности, выписанные ниже, и правила логического вывода из § 7 главы I), даны не для механического заучивания наизусть, но для осмысления основных логических законов и форм умозаключений. Целью должно являться понимание логических связей, рассуждений и доказательств, а не фотографическое воспроизведение мегабайт бесполезной информации.
Как будет показано ниже, законы логики важны для обеспечения механизма логических умозаключений: все правила логического вывода, применяемые человеком, используют те или иные законы логики. Ясно, что отрицание закона логики является противоречием, и наоборот – отрицание противоречия приводит к закону логики. Поэтому предыдущая теорема даёт и многочисленные примеры противоречий.
Разные по внешнему виду формулы могут иметь одинаковые таблицы истинности, в частности, теорема об основных законах логики даёт много тождественно истинных формул, принимающих только одно значение – 1. Формулы с одинаковыми таблицами истинности, отличаясь лексикографически, одинаковы с точки зрения логики. Поэтому оправдано следующее определение: формулы A(x1 , … , xk , y1 , … , ym) и B(y1 , … , ym , z1 , … , zn), где y1 , … , ym – все их общиепропозициональные переменные,называются равносильными, если при любых наборах значений переменных x1 , … , xk , y1 , … , ym , z1 , … , zn они принимают одинаковые значения. В этом случае пишут A º B.
Пример:A(x, z) = x Ú (x Ù z), B(x, y) = (x Ù y) Ú (x Ù 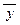 ).
).
Построим таблицы истинности этих формул от переменных x, y, z:
| x | y | z | x Ù z | A | x Ù y | 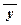
| x Ù 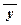
| B |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
Видно, что при любых значениях пропозициональных переменных x, y, z формулы A и В принимают одинаковые истинностные значения, так что A º B. С точки зрения истинности эти формулы неразличимы. При этом A º x, B º x.
Лемма (о свойствах отношения равносильности формул).Для любых формул А, В, С справедливы следующие утверждения:
(1) A º B тогда и только тогда, когда (A « B) – закон логики,
(2) A º A (рефлексивность равносильности),
(3) если А º В, то В º А (симметричность равносильности),
(4) если А º В и В º С, то А º С (транзитивность равносильности)
(5) если A º B, C º D, то 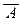 º
º 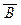 и для любой логической связки w Î {Ù , Ú , ® , «} верно (A w C) º (B w D), (С w A) º (D w B) .
и для любой логической связки w Î {Ù , Ú , ® , «} верно (A w C) º (B w D), (С w A) º (D w B) .
Доказательство. (1) Пусть вначале А º В. Рассмотрим таблицу истинности формулы A « B и любую её строку с интерпретацией e = (e1 ; … ; es ). По определению равносильности формул имеем А(e) = В(e), и значит, (А(e) « В(e)) = 1. Таким образом, формула (A « B) – закон логики.
Пусть наоборот, (A « B) – закон логики, т.е. при любой интерпретации e = (e1 ; … ; es ) верно А(e) = В(e), а значит, A º B.
(2), (3) очевидны.
(4) Пусть А º В и В º С. Тогда при любом наборе e = (e1 ; … ; es ) значений переменных верно А(e) = В(e) и В(e) = С(e), т.е. А(e) = С(e), A º C.
(5) Если A º B, C º D, то для любой интерпретации e = (e1 ; … ; es ) верно A(e) = B(e), С(e) = D(e). Поэтому 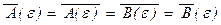 и для любой логической связки w Î {Ù , Ú , ® , «} имеем (A w C)(e) = (A(e) w C(e)) = = (B(e) w D(e)) = (B w D)(e). Аналогично и (C w A)(e) = (D w B)(e).
и для любой логической связки w Î {Ù , Ú , ® , «} имеем (A w C)(e) = (A(e) w C(e)) = = (B(e) w D(e)) = (B w D)(e). Аналогично и (C w A)(e) = (D w B)(e).
Лемма доказана.
Теорема (об основных равносильностях). Для любых формул A, B, C справедливы следующие равносильности:
(1) A º A (закон тождества),
(2) (A Ù A) º A (идемпотентность конъюнкции),
(A Ú A) º A (идемпотентность дизъюнкции),
(3) (A Ù B) º (B Ù A) (коммутативность конъюнкции),
(A Ú B) º (B Ú A) (коммутативность дизъюнкции),
(4) ((A Ù B) Ù C) º (A Ù (B Ù C)) (ассоциативность конъюнкции),
((A Ú B) Ú C) º (A Ú (B Ú C)) (ассоциативность дизъюнкции),
(5) ((A Ú B) Ù C) º ((A Ù С) Ú (B Ù C)) (законы дистрибутивности
((A Ù B) Ú C) º ((A Ú С) Ù (B Ú C)) конъюнкции и дизъюнкции),
(6) 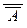 º A (закон двойного отрицания),
º A (закон двойного отрицания),
(7) 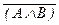 º (
º (  Ú
Ú 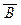 ) (законы
) (законы
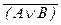 º (
º (  Ù
Ù 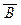 ) де Моргана),
) де Моргана),
(8) (A ® B) º ( 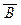 ®
®  ) (закон контрапозиции),
) (закон контрапозиции),
(9) (A « B) º ( 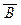 «
«  ) (закон противоположности),
) (закон противоположности),
(10) (A Ú (A Ù B)) º A (закон поглощения),
(11) (A Ù (A Ú B)) º A (закон ограничения),
(12) (A Ú (  Ù B)) º (A Ú B) (законы
Ù B)) º (A Ú B) (законы
(A Ù (  Ú B)) º (A Ù B) удаления),
Ú B)) º (A Ù B) удаления),
(13) (A Ù B) Ú (A Ù 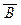 ) º A (закон склеивания
) º A (закон склеивания
(A Ú B) Ù (A Ú 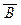 ) º A по В),
) º A по В),
(14) (A ® (B ® C)) º (B ® (A ® C)) (закон перестановки посылок),
(15) ((  ® B) Ù (
® B) Ù (  ®
® 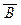 )) º A (закон рассуждений от противного),
)) º A (закон рассуждений от противного),
законы, выражающие одни логические связки через другие:
(16) (A ® B) º ( 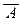 Ú B), (A ® B) º
Ú B), (A ® B) º 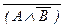 ,
,
(17) (A « B) º (A ® B) Ù (B ® A), (A « B) º 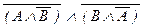 ,
,
(A « B) º 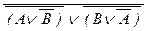 , (A « B) º (A Ù B) Ú (
, (A « B) º (A Ù B) Ú ( 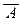 Ù
Ù 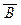 ),
),
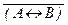 º (A Ù
º (A Ù 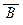 ) Ú (
) Ú (  Ù B),
Ù B),
(18) (A Ù B) º 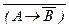 , (A Ù B) º
, (A Ù B) º 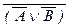 , A Ù
, A Ù 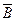 º
º 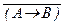 ,
,
(19) (A Ú B) º ( 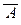 ® B), (A Ú B) º
® B), (A Ú B) º 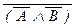 ,
,
законы действий с тавтологиями и противоречиями:
(20) (А Ù 1) º А, (A Ú 1) º 1,
(21) (А Ù 0) º 0, (A Ú 0) º A,
(22) (A Ù 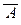 ) º 0, (A Ú
) º 0, (A Ú 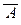 ) º 1,
) º 1,
(23) (A ® A) º 1, (0 ® A) º 1, (1 ® A) º A, (A ® 0) º 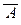 , (A ® 1) º 1,
, (A ® 1) º 1,
(24) (A « A) º 1, (A « 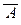 ) º 0, (A « 1) º A, (A « 0) º
) º 0, (A « 1) º A, (A « 0) º 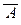 ,
,
(25) 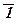 º 0,
º 0, 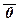 º 1.
º 1.
Доказательство. Упражняйтесь в построении таблиц истинности или примените теорему об основных законах логики и утверждение (1) леммы о свойствах отношения равносильности формул.
Приведённые в теореме простейшие равносильности вместе с утверждением (5) леммы о свойствах отношения равносильности формул позволяют упрощать формулы, точнее – находить для заданной формулы более простую, равносильную ей. Правда, понятие простоты субъективно, т.к. критерии простоты могут быть разными.
Примеры: 1. 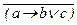 ® a º {(16)} º
® a º {(16)} º 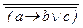 Ú a º {двойное отрицание} º (a ® (b Ú c))Ú a º {(16)} º (
Ú a º {двойное отрицание} º (a ® (b Ú c))Ú a º {(16)} º (  Ú b Ú c)Ú a º {ассоциативность} º º
Ú b Ú c)Ú a º {ассоциативность} º º  Ú b Ú c Ú a º {коммутативность} º (a Ú
Ú b Ú c Ú a º {коммутативность} º (a Ú  ) Ú b Ú c º {(22)} º 1 Ú (b Ú c) º º {(20)} º 1.
) Ú b Ú c º {(22)} º 1 Ú (b Ú c) º º {(20)} º 1.
2.(a ® b) ®  º {(16)} º (
º {(16)} º (  Ú b) ®
Ú b) ®  º {?!} º
º {?!} º 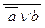 Ú
Ú  º {де Морган} º (
º {де Морган} º ( 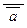 Ù
Ù 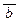 )Ú
)Ú  º {двойное отрицание} º (a Ù
º {двойное отрицание} º (a Ù 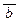 )Ú
)Ú  º {?!} º
º {?!} º  Ú
Ú 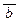 .
.
3. 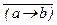 Ú (a ® c) Ù
Ú (a ® c) Ù  º {(16)} º
º {(16)} º 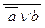 Ú ((
Ú (( 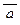 Ú c) Ù
Ú c) Ù 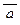 ) º {де Морган, ограничение} º
) º {де Морган, ограничение} º 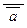 Ù
Ù 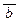 Ú
Ú  º {двойное отрицание} º (a Ù
º {двойное отрицание} º (a Ù 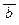 ) Ú
) Ú  º {дистрибутивность} º (a Ú
º {дистрибутивность} º (a Ú  ) Ù (
) Ù ( 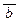 Ú
Ú  ) º {(22)} º 1 Ù (
) º {(22)} º 1 Ù ( 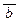 Ú
Ú  ) º {(20)} º
) º {(20)} º 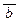 Ú
Ú  .
.
4. ((  « c)® b)Ú a Ú c º {(16)} º
« c)® b)Ú a Ú c º {(16)} º 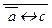 Ú b Ú a Ú c º {(17)} º º
Ú b Ú a Ú c º {(17)} º º 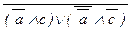 Ú b Ú a Ú c º {де Морган} º (a Ú
Ú b Ú a Ú c º {де Морган} º (a Ú 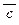 ) Ù (
) Ù (  Ú c) Ú b Ú a Ú c º º {дистрибутивность, 0, 1} º (a Ù c Ú
Ú c) Ú b Ú a Ú c º º {дистрибутивность, 0, 1} º (a Ù c Ú 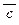 Ù
Ù  )Ú b Ú a Ú c º {ассоциативность, коммутативность, поглощение} º
)Ú b Ú a Ú c º {ассоциативность, коммутативность, поглощение} º  Ù
Ù 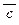 Ú b Ú (a Ú c) º {коммутативность} º º (a Ú
Ú b Ú (a Ú c) º {коммутативность} º º (a Ú  Ù
Ù 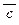 )Ú c Ú b º {удаление} º (a Ú
)Ú c Ú b º {удаление} º (a Ú 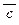 ) Ú c Ú b º {(22)} º a Ú 1 Ú b º º {(20)} º 1.
) Ú c Ú b º {(22)} º a Ú 1 Ú b º º {(20)} º 1.
Общий алгоритм упрощения формул сформулировать затруднительно, поскольку нет общепринятого критерия простоты формулы. Однако предыдущие примеры показывают, что в равносильных преобразованиях формул можно выделить следующие этапы:
1.избавляемся от импликаций и эквивалентностей, используя равносильности A ® B º 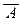 Ú B и A « B º (A Ù B) Ú (
Ú B и A « B º (A Ù B) Ú ( 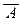 Ù
Ù 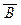 ),
),
2.избавляемся от длинных отрицаний (т.е. отрицаний, стоящих не над переменными) с помощью законов де Моргана: 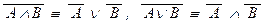 ,
,
3.избавляемся от многократных отрицаний (двукратных и более) с помощью закона двойного отрицания 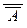 º A,
º A,
После этих преобразований получим формулу, записанную с помощью конъюнкций, дизъюнкций и коротких отрицаний, стоящих над пропозициональными переменными. На эту формулу можно смотреть как на алгебраическое выражение от переменных x1 , … , xn , 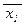 , … ,
, … , 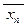 . При этом ввиду законов дистрибутивности можно равноправно считать, что роль сложения выполняет операция Ú дизъюнкции, а роль умножения – операция Ù конъюнкции, или же наоборот: роль сложения выполняет операция Ù конъюнкции, а роль умножения – операция Ú дизъюнкции.
. При этом ввиду законов дистрибутивности можно равноправно считать, что роль сложения выполняет операция Ú дизъюнкции, а роль умножения – операция Ù конъюнкции, или же наоборот: роль сложения выполняет операция Ù конъюнкции, а роль умножения – операция Ú дизъюнкции.
4.если считать, что Ú – аналог сложения, а Ù – умножения, то раскрывая скобки (по дистрибутивности) и учитывая законы коммутативности А Ú В º В Ú А, А Ù В º В Ù А, идемпотентности А Ú А º А, А Ù А º А, и правила действий с противоречиями, приведём формулу к дизъюнктивной форме (ДФ) 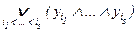 , где каждое yi – либо переменная xi , либо её отрицание
, где каждое yi – либо переменная xi , либо её отрицание 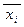 . Эту дизъюнктивную форму иногда можно ещё более упростить,
. Эту дизъюнктивную форму иногда можно ещё более упростить,
применяя законы поглощения A Ú (A Ù B) º A, удаления A Ú ( 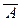 Ù B) º A Ú B
Ù B) º A Ú B
и склейки (A Ù B) Ú (A Ù 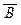 ) º A.
) º A.
5.если считать, что Ù – аналог сложения, а Ú – умножения, то раскрывая скобки (по дистрибутивности) и учитывая законы коммутативности А Ú В º В Ú А, А Ù В º В Ù А, идемпотентности А Ú А º А, А Ù А º А, и правила действий с тавтологиями, получим конъюнктивную форму (КФ) 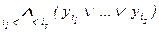 , где каждое yi – либо переменная xi , либо её отрицание
, где каждое yi – либо переменная xi , либо её отрицание 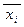 . Эту конъюнктивную форму можно ещё более упростить, применяя законы A Ù (A Ú B) º A, A Ù (
. Эту конъюнктивную форму можно ещё более упростить, применяя законы A Ù (A Ú B) º A, A Ù ( 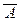 Ú B) º A Ù B и (A Ú B) Ù (A Ú
Ú B) º A Ù B и (A Ú B) Ù (A Ú 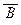 ) º A.
) º A.
Пример: Привести формулу x ® y « 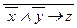 к дизъюнктивной и конъюнктивной формам.
к дизъюнктивной и конъюнктивной формам.
x ® y « 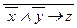 = (x ® y) «
= (x ® y) « 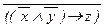 º (
º (  Ú y) «
Ú y) « 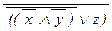 º
º
º (  Ú y) «
Ú y) «  Ù
Ù  Ù
Ù 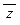 º ((
º ((  Ú y) Ù
Ú y) Ù  Ù
Ù  Ù
Ù  ) Ú (
) Ú ( 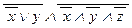 ) º
) º
º ((  Ú y) Ù
Ú y) Ù  Ù
Ù  Ù
Ù  ) Ú (x Ù
) Ú (x Ù  Ù (x Ú y Ú z)).
Ù (x Ú y Ú z)).
Дизъюнктивная форма (ДФ): ((  Ú y) Ù
Ú y) Ù  Ù
Ù  Ù
Ù  ) Ú (x Ù
) Ú (x Ù  Ù (x Ú y Ú z)) º
Ù (x Ú y Ú z)) º
º (((  Ù
Ù  Ù
Ù  Ù
Ù  ) Ú (y Ù
) Ú (y Ù  Ù
Ù  Ù
Ù  )) Ú (x Ù
)) Ú (x Ù 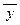 Ù (x Ú y Ú z)) º
Ù (x Ú y Ú z)) º
º ((  Ù
Ù  Ù
Ù  ) Ú 0) Ú (x Ù
) Ú 0) Ú (x Ù 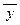 Ù (x Ú y Ú z)) º
Ù (x Ú y Ú z)) º
º (  Ù
Ù  Ù
Ù  )Ú (x Ù
)Ú (x Ù 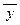 Ù (x Ú y Ú z)) º
Ù (x Ú y Ú z)) º
º (  Ù
Ù  Ù
Ù  ) Ú ((x Ù
) Ú ((x Ù 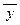 Ù x) Ú (x Ù
Ù x) Ú (x Ù 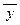 Ù y) Ú (x Ù
Ù y) Ú (x Ù 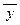 Ù z)) º
Ù z)) º
º (  Ù
Ù  Ù
Ù  ) Ú ((x Ù
) Ú ((x Ù  ) Ú (x Ù
) Ú (x Ù 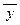 Ù z)) º (
Ù z)) º (  Ù
Ù  Ù
Ù  ) Ú (x Ù
) Ú (x Ù  ) º
) º
º ((  Ù
Ù  ) Ú x ) Ù
) Ú x ) Ù 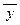 º (x Ú
º (x Ú 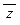 ) Ù
) Ù 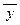 º (x Ù
º (x Ù 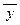 ) Ú (
) Ú ( 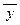 Ù
Ù 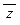 ) – ДФ.
) – ДФ.
Конъюнктивная форма (КФ): (( 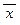 Ú y) Ù
Ú y) Ù  Ù
Ù  Ù
Ù  ) Ú (x Ù
) Ú (x Ù  Ù (x Ú y Ú z)) º
Ù (x Ú y Ú z)) º
º ((  Ú y) Ú x) Ù ((
Ú y) Ú x) Ù ((  Ú y) Ú
Ú y) Ú  ) Ù ((
) Ù ((  Ú y) Ú (x Ú y Ú z)) Ù
Ú y) Ú (x Ú y Ú z)) Ù
Ù ( 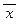 Ú x) Ù (
Ú x) Ù (  Ú
Ú  ) Ù (
) Ù (  Ú (x Ú y Ú z)) Ù
Ú (x Ú y Ú z)) Ù
Ù (  Ú x) Ù (
Ú x) Ù (  Ú
Ú  ) Ù (
) Ù (  Ú (x Ú y Ú z)) Ù
Ú (x Ú y Ú z)) Ù
Ù (  Ú x) Ù (
Ú x) Ù (  Ú
Ú  ) Ù (
) Ù (  Ú (x Ú y Ú z)) º
Ú (x Ú y Ú z)) º
º (1 Ù 1 Ù 1) Ù (1 Ù (  Ú
Ú  ) Ù 1) Ù ((
) Ù 1) Ù ((  Ú x) Ù
Ú x) Ù  Ù 1) Ù
Ù 1) Ù
Ù ((  Ú x)Ù (
Ú x)Ù (  Ú
Ú  )Ù 1) º
)Ù 1) º
º (  Ú
Ú  ) Ù (
) Ù (  Ú x) Ù
Ú x) Ù  Ù (
Ù (  Ú x) Ù (
Ú x) Ù (  Ú
Ú 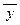 ) º
) º
º  Ù (
Ù (  Ú x) Ù (
Ú x) Ù (  Ú
Ú  ) º (
) º (  Ú x) Ù
Ú x) Ù  Ù (
Ù (  Ú
Ú  ) º (
) º ( 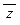 Ú x) Ù
Ú x) Ù  – КФ.
– КФ.
Дата добавления: 2021-12-14; просмотров: 492;











