Примеры формул и не формул
| Формулы | Использованные правила | Не формулы | Нарушенные правила |
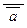
| a (Ф1)
 (Ф2) (Ф2)
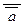 (Ф2) (Ф2)
| 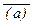
| (a) – не формула (Ф2) |
| (a Ú b) | a (Ф1) b (Ф1) (a Ú b) (Ф2) | ab | (Ф2) |
( 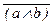 ® c) ® c)
| a (Ф1)
b (Ф1)
c (Ф1)
(a Ù b) (Ф2)
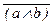 (Ф2)
( (Ф2)
( 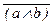 ® c) (Ф2) ® c) (Ф2)
| a Ú b Ù c | нет скобок (Ф2) |
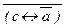
| a (Ф1)
c (Ф1)
 (Ф2)
(с « (Ф2)
(с «  ) (Ф2) ) (Ф2)
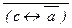 (Ф2) (Ф2)
| 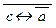
| с «  – не формула
(Ф2) – не формула
(Ф2)
|
Итак, введённое понятие формулы исчисления высказываний позволяет из элементарных высказываний, которые можно подставлять вместо пропозициональных переменных, строить более сложные высказывания с помощью естественных языковых конструкций, используя логические связки и разделительные скобки.
Несмотря на то, что отсутствие скобок является ошибкой при написании формулы, самые внешние скобки в формуле можно опустить, не нарушая её смысла. Поэтомув дальнейшем для упрощения записи условимся в формулах допускать отсутствие самых внешних скобок (их всегда можно поставить, восстановив status quo). Таким образом, по-прежнему ошибочна запись a Ú b Ù c, но допустимо выражение с « 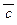 , т.к. оно станет формулой после добавления внешних скобок: (с «
, т.к. оно станет формулой после добавления внешних скобок: (с « 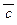 ).
).
Иногда для экономии места применяют следующее правило восстановления скобок по умолчанию:
(С1): скобки в формуле расставляются в несколько проходов, рассматривая входящие в неё символы слева направо.
(С2): на каждом проходе обрабатываются логические связки одного из типов в соответствии с их приоритетами: 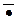 , Ù , Ú , ® , « (это значит, что двигаясь слева направо, вначале находят первое ещё не обработанное отрицание и обрабатывают его в соответствии с правилом (С3), при отсутствии таковых – первую ещё не обработанную конъюнкцию, затем – дизъюнкцию, далее – импликацию и, наконец, эквивалентность, и.т.д).
, Ù , Ú , ® , « (это значит, что двигаясь слева направо, вначале находят первое ещё не обработанное отрицание и обрабатывают его в соответствии с правилом (С3), при отсутствии таковых – первую ещё не обработанную конъюнкцию, затем – дизъюнкцию, далее – импликацию и, наконец, эквивалентность, и.т.д).
(С3): обработка отрицания состоит в расстановке всех скобок в формуле, стоящей под этим отрицанием (в соответствии с правилами (С1)–(С4)).
(С4): обработка остальных логических связок w Î {Ù , Ú , ® , «} состоит в нахождении их минимальных формул-аргументов Ф1 , Ф2 и расстановке внешних скобок для получения выражения (Ф1 w Ф2).
Проиллюстрируем это правило на нескольких примерах:
Примеры: 1. Для выражения a Ú b Ù c после первого прохода получится выражение a Ú (b Ù c) – конъюнкция обрабатывается раньше дизъюнкции, а при втором проходе – формула (a Ú (b Ù c)).
2. Для выражения a ® b Ù c « c Ù d ® a результаты проходов таковы:
а. a ® (b Ù c) « (c Ù d) ® a (обработано две конъюнкции),
б. (a ® (b Ù c)) « ((c Ù d) ® a) (обработано две импликации),
в. ((a ® (b Ù c)) « ((c Ù d) ® a)) (обработана эквивалентность).
3. Для выражения a ® b Ù (c « c) Ù d ® a результаты будут следующими:
а. a ® ((b Ù (c « c)) Ù d) ® a (обработано две конъюнкции),
б. ((a ® ((b Ù (c « c)) Ù d)) ® a) (обработано две импликации).
4. Для выражения 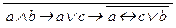 Ú a Ù bÚ
Ú a Ù bÚ 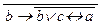 результаты проходов таковы:
результаты проходов таковы:
а. 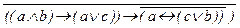 Ú a Ù bÚ
Ú a Ù bÚ 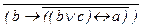
(обработано два отрицания),
б. 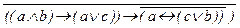 Ú (a Ù b)Ú
Ú (a Ù b)Ú 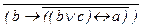
(обработана конъюнкция),
в. (( 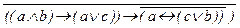 Ú (a Ù b))Ú
Ú (a Ù b))Ú 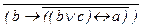 )
)
(обработано две дизъюнкции).
Итак, в дальнейшем, если некоторое выражение в алфавите языка исчисления высказываний не является формулой по причине отсутствия некоторых скобок, то это выражение можно пытаться превратить в формулу, расставляя в нём недостающие скобки с помощью описанного выше правила.
Дата добавления: 2021-12-14; просмотров: 404;











