Истинностные значения формул
Истинность или ложность элементарных высказываний оставляется на совести той области знания, к которой они относятся. Логика позволяет по заданным истинностным значениям элементарных высказываний вычислять истинностные значения построенных из них сложных высказываний.
Прежде, чем переходить к формальным рассуждениям, введём следующие соглашения: вместо значения истина будем писать 1, а вместо значения ложь – 0. Интерпретацией формулыA(x1 , … , xn) назовём любой набор e = (e1 ; … ; en) значений переменных x1 = e1 , … , xn = en (ei Î {0, 1}, 1 £ i £ n).
Теперь любой формуле исчисления высказываний A(x1 , … , xn) от пропозициональных переменных x1 , … , xn можно присвоить истинностное значение A(e) = A(e1 , … , en ) Î {0, 1} при данной интерпретации e = (e1 ; … ; en) по следующим правилам:
(И1): если A(x1 , … , xn) – одна из пропозициональных переменных x1 , … , xn , то её истинностное значение уже определено: в случае A(x1 , … , xn) = xi полагаем A(e) = ei ;
(И2): если A(x1 , … , xn) = (B(x1 , … , xn) w C(x1 , … , xn)) или A(x1 , … , xn) = = 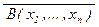 , где w – одна из логических связок Ù , Ú , ® , « (т.е. формула A(x1 , … , xn) получена из более простых формул B(x1 , … , xn) и C(x1 , … , xn) с помощью одной из конструкций правила образования формул (Ф2)), а значения B(e) = B(e1 , … , en ) и C(e) = С(e1 , … , en ) уже вычислены, то истинностное значение A(e) = A(e1 , … , en ) приписывается с помощью следующих аксиом логических связок:
, где w – одна из логических связок Ù , Ú , ® , « (т.е. формула A(x1 , … , xn) получена из более простых формул B(x1 , … , xn) и C(x1 , … , xn) с помощью одной из конструкций правила образования формул (Ф2)), а значения B(e) = B(e1 , … , en ) и C(e) = С(e1 , … , en ) уже вычислены, то истинностное значение A(e) = A(e1 , … , en ) приписывается с помощью следующих аксиом логических связок:
| B(e) | C(e) | 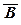 (e) (e)
| (B(e) Ù C(e)) | (B(e) Ú C(e)) | (B(e) ® C(e)) | (B(e) « C(e)) |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 |
Следует подчеркнуть, что законы вычисления этих логических связок являются именно аксиомами – они принимаются на веру. Часть из них согласуется со здравым смыслом и интуитивными описаниями значения логических связок. Некоторые значения менее очевидны, и осознание необходимости их использования нуждается в дополнительных аргументах, которые рождаются только в результате работы мысли.
Наиболее трудна для понимания аксиома вычисления импликации, в частности, нуждается в дополнительных аргументах тот факт, что при ложной посылке B(e) значение импликации всегда истинно. По смыслу логическая связка импликация ® означает следование, выводимость. Таким образом, нужно понять, почему из ложного утверждения выводится любое другое. В связи с этим невозможно не упомянуть случай, произошедший с Бертраном Расселом – известным специалистом по математической логике XX в. Он читал лекцию для философов, когда один из них попросил объяснить, почему из ложного утверждения можно вывести всё, что угодно ? Тогда Рассел для примера доказал, что из утверждения 2´2 = 5 следует, что он – Папа Римский. Вот это остроумное доказательство:
2´2 = 5, 2+2 = 2+3, 2 = 3, 1+1 = 2+1, 1 = 2,
Рассел и Папа Римский – их двое, но 2 = 1, так что они – одно лицо, ч.т.д.
Отметим ещё, что значение импликации огромно: любое научное утверждение формулируется в импликативном виде, т.е. в виде импликации A ® B. Например, теорема Пифагора “сумма квадратов катетов равна квадрату гипотенузы” на самом деле означает следующее: если ABC – треугольник с прямым углом C, то AB2 = AC2 + BC2. Точно так же формулируются и утверждения других наук: в них всегда должна присутствовать посылка А и заключение В, а само утверждение означает истинность импликации A ® B. Если посылка А истинна, то истинность импликации означает истинность заключения В. Если же посылка ложна, то импликация всё равно истинна. Поэтому, если вдруг выяснилось, что В ложно, это ещё не значит, что нарушен закон той или иной науки, просто, возможно, посылка А стала ложной, а импликация всё равно истинна.
Как с помощью сформулированных аксиом вычислить значение любой формулы при заданных значениях её пропозициональных переменных ? Значение формулы вычисляется последовательно, начиная со значений пропозициональных переменных в соответствии с построением самой формулы по правилу (Ф2) с применением на каждом шаге описанных выше аксиом.
Примеры: 1. Вычислить значение формулы (  Ú b) при a = 1, b = 0.
Ú b) при a = 1, b = 0.
Формула (  Ú b) построена из формул
Ú b) построена из формул  и b путём применением конструкции (A Ú B) правила (Ф2).Поэтому вначале нужно вычислить значения формул
и b путём применением конструкции (A Ú B) правила (Ф2).Поэтому вначале нужно вычислить значения формул  и b, а затем применить аксиому вычисления дизъюнкции. Значение b = 0 дано, а значение формулы
и b, а затем применить аксиому вычисления дизъюнкции. Значение b = 0 дано, а значение формулы  вычисляется из заданного значения формулы a по аксиоме значения отрицания:
вычисляется из заданного значения формулы a по аксиоме значения отрицания: 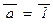 = 0. Таким образом, по аксиоме значения дизъюнкции получаем в итоге (
= 0. Таким образом, по аксиоме значения дизъюнкции получаем в итоге (  Ú b) = (0 Ú 0) = 0.
Ú b) = (0 Ú 0) = 0.
Следует отметить, что при других наборах значений переменных значение этой же формулы может быть другим. Например, если a = 0 = b, то  = 1 и (
= 1 и (  Ú b) = (1 Ú 0) = 1.
Ú b) = (1 Ú 0) = 1.
2. Вычислить значение формулы ( 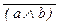 ® c) при a = 1, b = 1, c = 0 .
® c) при a = 1, b = 1, c = 0 .
Опишем процесс построения формулы по правилу (Ф2), одновременно вычисляя на каждом шаге истинностные значения получаемых формул при заданных значениях пропозициональных переменных: a = 1, b = 1, c = 0, (a Ù b) = 1, 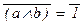 =0, (
=0, ( 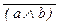 ® c) = (0 ® 0) = 1. Таким образом, искомое значение равно 1.
® c) = (0 ® 0) = 1. Таким образом, искомое значение равно 1.
Для a = 0, b = 0, с = 0 получим (a Ù b) = (0 Ù 0) = 0, 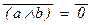 =1, (
=1, ( 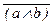 ® c) = (1® 0) = 0.
® c) = (1® 0) = 0.
Предыдущие примеры показывают, что значение формулы зависит от конкретного набора её пропозициональных переменных, т.е. от конкретной интерпретации формулы: при разных интерпретациях значения формулы могут быть различными. Поэтому говорить об истинности или ложности формулы, не указывая интерпретации, бессмысленно.
| x1 | … | xn | … | A(x1 , … , xn ) |
| … | … | … | … | … |
| e1 | … | en | … | A(e1 , … , en ) |
| … | … | … | … | … |
На практике обычно заранее неизвестно, какие именно значения принимают пропозициональные переменные. Поэтому для нахождения всех истинностных значений формулы A(x1 , … , xn ) строят её таблицу истинности, т.е. таблицу указанного слева вида, которая имеет (как будет показано ниже) 2n строк, каждая из которых в первых n столбцах содержит конкретные значения e1 , … , en пропозициональных переменных x1 , … , xn , в последующих столбцах – вычисленные промежуточные значения более простых формул, из которых строится рассматриваемая формула, а в последнем столбце – значение формулы A(x1 , … , xn ) при интерпретации e = (e1 ; … ; en) . При этом в первых n столбцах таблицы истинности должны быть ровно по одному разу перечислены все возможные наборы значений пропозицииональных переменных x1 , … , xn .
Примеры: 1. Строим таблицы истинности формул  Ú b и
Ú b и 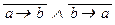 .
.
| a | b | 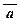
| 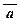 Ú b Ú b
| a | b | a ® b | 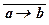
| b ® a | 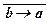
| 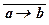 Ù Ù 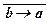
| |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| a | b | c | 2 | |||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
2. Построим таблицу истинности для формулы ((a Ù b) Ú c) « ((a Ú c) Ù (b Ú c)).
В ней цифрами обозначены формулы: 1 = (a Ù b), 2 = (1Ú c), 3 = (a Ú c), 4= (b Ú c), 5= (3Ù 4), 6 = 2« 5. Такие сокращения удобны для построения таблиц истинности громоздких формул. Использованные в обозначениях числа определяют и порядок вычислений.
Для того чтобы успешно строить таблицы истинности формул, нужно иметь алгоритм перечисления всех возможных наборов значений n её пропозициональных переменных x1 , … , xn . Можно воспользоваться, например, двоичной системой счисления: каждая интерпретация e = (e1 ; … ; en ) отождествляется с двоичным числом 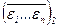 из n двоичных цифр e1 , … , en Î {0, 1}, которое в десятичном виде выглядит как e1×2n–1 + … + en×20. Наименьшее число 0 = 0 … 02 = = 0×2n–1+…+0×20 соответствует интерпретации e = (0 ; … ; 0 ), а наибольшее 1 … 12 = 1×2n–1+…+1×20 = 2n–1+2n–2+…+2+1 =
из n двоичных цифр e1 , … , en Î {0, 1}, которое в десятичном виде выглядит как e1×2n–1 + … + en×20. Наименьшее число 0 = 0 … 02 = = 0×2n–1+…+0×20 соответствует интерпретации e = (0 ; … ; 0 ), а наибольшее 1 … 12 = 1×2n–1+…+1×20 = 2n–1+2n–2+…+2+1 = 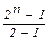 = 2n – 1 (по формуле суммирования геометрической прогрессии) – интерпретации e = (1 ; … ; 1). Поэтому для перечисления всех интерпретаций достаточно использовать двоичные
= 2n – 1 (по формуле суммирования геометрической прогрессии) – интерпретации e = (1 ; … ; 1). Поэтому для перечисления всех интерпретаций достаточно использовать двоичные
| 0 | 00000 | 8 | 01000 | 16 | 10000 | 24 | 11000 |
| 1 | 00001 | 9 | 01001 | 17 | 10001 | 25 | 11001 |
| 2 | 00010 | 10 | 01010 | 18 | 10010 | 26 | 11010 |
| 3 | 00011 | 11 | 01011 | 19 | 10011 | 27 | 11011 |
| 4 | 00100 | 12 | 01100 | 20 | 10100 | 28 | 11100 |
| 5 | 00101 | 13 | 01101 | 21 | 10101 | 29 | 11101 |
| 6 | 00110 | 14 | 01110 | 22 | 10110 | 30 | 11110 |
| 7 | 00111 | 15 | 01111 | 23 | 10111 | 31 | 11111 |
коды чисел от 0 до 2n – 1, которые приведены в таблице (n = 5).
Здесь использована пятиразрядная двоичная запись чисел, но незначащие нули по мере необходимости можно отбросить так же, как это сделано в приводимых ниже примерах перечисления интерпретаций для n = 1, 2, 3, 4.
Примеры:n = 1: 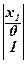 , n =2:
, n =2: 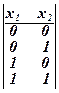 , n = 3:
, n = 3: 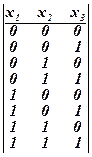 , n = 4:
, n = 4: 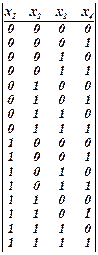
Теорема (о правиле перечисления интерпретаций).В таблице, построенной путём выписывания n-значных двоичных кодов всех чисел от 0 до 2n – 1, перечисляются ровно по одному разу всевозможные наборы значений n пропозициональных переменных.
Доказательство. Как было отмечено, каждой интерпретации e = (e1 ; … ; en ) соответствует двоичное число 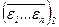 из n двоичных цифр e1 , … , en , которое находится в диапазоне от 0 до 2n – 1. При этом разным интерпретациям будут отвечать и разные числа: если e = (e1 ; … ; en ) ¹ (d1 ; … ; dn) = d, то
из n двоичных цифр e1 , … , en , которое находится в диапазоне от 0 до 2n – 1. При этом разным интерпретациям будут отвечать и разные числа: если e = (e1 ; … ; en ) ¹ (d1 ; … ; dn) = d, то 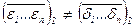 . Кроме того, в результате такого сопоставления будут перечислены без пропусков все двоичные числа от 0 до 2n – 1 : число
. Кроме того, в результате такого сопоставления будут перечислены без пропусков все двоичные числа от 0 до 2n – 1 : число 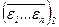 появится при рассмотрении интерпретации e = (e1 ; … ; en ).
появится при рассмотрении интерпретации e = (e1 ; … ; en ).
Теорема доказана.
Следствие (о количественаборов из нулей и единиц длины n).Количество всевозможных наборов длины n из нулей и единиц равно 2n . Столько же и строк в любой таблице истинности формулы от n переменных.
Доказательство очевидно, т.к. количество всевозможных наборов длины n из нулей и единиц равно количеству всевозможных интерпретаций для n пропозициональных переменных, которое (ввиду доказанной теоремы) равно количеству чисел от 0 до 2n – 1, т.е. 2n. Следствие доказано.
Следствие (о количестве подмножеств n-элементного множества).Любое n-элементное множество содержит 2n подмножеств.
Доказательство. Пусть дано множество A = {a1 , … , an }. Каждому его подмножеству X Í A сопоставим набор (e1 ; … ; en ) из нулей и единиц длины n, полностью определяющий это подмножество. Для этого положим ei = 1, если ai Î X, и ei = 0, если ai Ï X (1 £ i £ n). Кстати, именно такой способ интерпретации множеств реализуется в некоторых языках программирования.
Примеры:Для множества A = {a1 , a2 , a3 } подмножеству Х = {a1 , a3} будет соответствовать набор (1; 0; 1), а подмножеству Х = {a2 } – набор (0; 1; 0). Пустому подмножеству (не содержащему элементов) будет сопоставлен набор (0; 0; 0), а всему множеству А – набор (1; 1; 1).
Легко понять, что по любому набору (e1 ; … ; en ) из нулей и единиц длины n однозначно восстанавливается соответствующее ему подмножество: именно в множестве X нужно собрать все те элементы ai , для которых ei = 1 (1 £ i £ n). Поэтому подмножеств в n-элементном множестве будет столько, сколько существует наборов из нулей и единиц длины n, т.е. 2n. Следствие доказано.
Пример. Перечислим все подмножества 4-элементного множества.
Будем перечислять подмножества, выписывая соответствующие им наборы нулей и единиц, построенные по двоичным числам из диапазона от 0 до 24 = 16:
| № | набор | подмножество | № | набор | подмножество |
| (0; 0; 0; 0) | Æ | (1; 0; 0; 0) | {a1 } | ||
| (0; 0; 0; 1) | {a4 } | (1; 0; 0; 1) | {a1 , a4 } | ||
| (0; 0; 1; 0) | {a3 } | (1; 0; 1; 0) | {a1 , a3 } | ||
| (0; 0; 1; 1) | {a3 , a4 } | (1; 0; 1; 1) | {a1 , a3 , a4 } | ||
| (0; 1; 0; 0) | {a2 } | (1; 1; 0; 0) | {a1 , a2 } | ||
| (0; 1; 0; 1) | {a2 , a4 } | (1; 1; 0; 1) | {a1 , a2 , a4 } | ||
| (0; 1; 1; 0) | {a2 , a3 } | (1; 1; 1; 0) | {a1 , a2 , a3 } | ||
| (0; 1; 1; 1) | {a2 , a3 , a4 } | (1; 1; 1; 1) | {a1 , a2 , a3 , a4 } |
Дата добавления: 2021-12-14; просмотров: 443;











