Язык исчисления высказываний

В любом естественном языке есть возможность строить из простых высказываний более сложные.

Примеры: 1. “Сейчас температура воздуха на улице от –25 до –30 градусов Цельсия”, “5 – простое число”, “Сегодня скорость ветра в г. Тобольске больше 5 м / сек.” – всё это элементарные высказывания.

2. “Сейчас температура воздуха на улице от –25 до –30 градусов Цельсия” и “5 – простое число”; Если “сегодня скорость ветра в г. Тобольске больше 5 м / сек.”, то “5 – простое число”; Неверно, что “5 – простое число”, “5 – простое число” тогда и только тогда, когда “Сейчас температура воздуха на улице от –25 до –30 градусов Цельсия”; “Сейчас температура воздуха на улице от –25 до –30 градусов Цельсия” или “Сегодня скорость ветра в г. Тобольске больше 5 м / сек.” – всё это сложные высказывания, полученные из предыдущих с помощью специальных языковых конструкций.

Говоря формально, некоторые из использованных в этих примерах утверждений высказываниями не являются: их невозможно соотнести с действительностью, поскольку они не содержат полной информации о констатируемом факте. Например, не ясно ни где именно измеряется температура воздуха или скорость ветра, ни когда именно это происходило. Такое положение дел присуще большинству из используемых в быту “высказываний”. Если мы, общаясь, понимаем друг друга, то благодаря тому, что воспринимаем “высказывания” собеседника по умолчанию с местом действия “здесь” и временем действия – “сейчас”.

Не дело математики и, в частности, логики выяснять истинность или ложность высказываний, оперирующих понятиями из других областей знания или жизненного опыта. Логика даёт средства для построения из элементарных высказываний, ответственность за истинность или ложность которых лежит на пользователе каждой науки, более сложных высказываний, а также – для построения истинностных значений этих сложных высказываний в зависимости от истинностных значений элементарных высказываний, из которых они построены. Для этого создан специальный язык исчисления высказываний, к изучению которого, мы и переходим.

Для обозначения элементарных высказываний будем использовать, как правило, малые буквы доступных алфавитов, с индексами или без них: a, b, c, d, … … , б₃₄₅ , … , которые будем называть пропозициональными переменными или просто переменными.

Для построения более сложных осмысленных выражений используют следующие специальные знаки, называемые логическими связками:

Знак	Название	Языковой аналог	Использование
Ù	конъюнкция	A и B	A Ù B
Ú	дизъюнкция	A или B	A Ú B
®	импликация	если A , то B	A ® B
«	эквивалентность	A тогда и только тогда, когда B	A « B
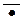
	отрицание	неверно, что A

Наконец, как и во всяком языке, в языке исчисления высказываний будут использоваться служебные символы– скобки: левая скобка ( и правая скобка ).

Таким образом, алфавит языка исчисления высказываний состоит из трёх описанных выше групп символов: пропозициональных переменных, логических связок и служебных символов.

Кроме того, язык исчисления высказываний, как и любой естественный язык, предполагает наличие правил конструирования фраз – осмысленных предложений языка, состоящих из слов. Слова состоят из букв, но не всякая комбинация букв является словом, и не всякий набор слов образует фразу. В языке исчисления высказываний осмысленными фразами служат формулы.

Понятие формулы языка исчисления высказыванийстроится от простого к сложному с помощью следующих трёх правил:

(Ф1): любая пропозициональная переменная является формулой.

(Ф2): если A и В – формулы, то (A Ù B), (A Ú B), (A ® B), (A « B), 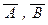– тоже формулы.

(Ф3): других формул нет.

Процесс построения формул похож на игру в детский конструктор, в котором дан набор деталей (правило (Ф1) о пропозициональных переменных), соединительные узлы (правило (Ф2) о логических связках), а в остальном предоставлена полная свобода конструирования предоставленными средствами (ограничительное правило (Ф3)).