Логическое следование

Понятие логического следования является одним из важнейших в математической логике и имеет непосредственное отношение к жизни. Нам часто приходится обосновывать те или иные утверждения: это значит, что на основании нескольких высказываний a₁ , … , a_n – посылок, делается вывод: “следовательно, верно утверждение (заключение) а”. Такой вывод является корректным в том и только том случае, если из истинности всех посылок следует истинность заключения, т.е. если истинно высказывание “если a₁ и a₂ , и … , и a_n , то a”. Это приводит к следующему определению логического следствия.

Пусть А₁ , … , A_n , A – формулы исчисления высказываний от переменных x₁ , … , x_k , Г = {А₁ , … , A_n }. Говорят, что формула А является логическим следствием множества формул Г (или просто формул А₁ , … , A_n), если при любых интерпретациях e = (e₁ ; … ; e_k ) со свойством A₁(e) = … = A_n(e) = 1 выполнено условие A(e) = 1. В этом случае пишут А₁ , … , A_n 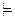A или кратко Г 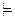А. Последнее обозначение используется и в случае Г = Æ : пишут 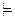А, понимая под этим, что А – закон логики.

Примеры: 1. Будет ли a ® b логическим следствием формул 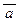, b ?

a	b		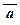a ® b
0	0	1	1
1	0	0	0
0	1	1	1
1	1	0	1

Построим общую таблицу истинности для формул 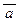, b, a ® b и проверим выполнение требований определения логического следования. Видно, что в таблице ровно при одной интерпретации (a = 0, b = 1) обе формулы-посылки 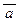и b принимают значение 1. При этом значение формулы a ® b также равно 1, т.е. формула a ® b является логическим следствием формул 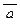и b.

2.Будет ли формула a « b Ú с логическим следствием формул 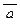, a ® b, b Ù c ?

Аналогично предыдущему, строим таблицу истинности и замечаем, что ровно

a	b	c		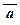a ® b	b Ù c	b Ú c	a « b Ú с
0	0	0	1	1	0	0	1
0	0	1	1	1	0	1	0
0	1	0	1	1	0	1	0
0	1	1	1	1	1	1	0
1	0	0	0	0	0	0	0
1	0	1	0	0	0	1	1
1	1	0	0	1	0	1	1
1	1	1	0	1	1	1	1

при одной интерпретации (a = 0, b = 1 = c) все формулы 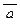, a ® b, b Ù c принимают значение 1. Однако при этой интерпретации фор­мула-заключение a « b Ú с принимает значение 0, так что она не является логическим следствием формул 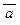, a ® b и b Ù c.

Теорема (критерий логического следования).Для формул А₁ , … , A_n и А условие А₁ , … , A_n 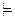A выполнено тогда и только тогда, когда формула (А₁ Ù … Ù A_n) ® A является законом логики.

Доказательство. Пусть выполнено А₁ , … , A_n 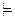A. Докажем, что формула (А₁ Ù … Ù A_n ® A) – закон логики. При каких интерпретациях e = (e₁ ; … ; e_k) рассматриваемая формула может быть ложна ? Только при тех, для которых верно (А₁ Ù … Ù A_n)(e) = 1, но А(e) = 0. Это значит, что A₁(e ) = … = A_n(e) = 1, но A(e) = 0 – противоречие с условием А₁ , … , A_n 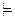A. Поэтому рассматриваемая формула (А₁ Ù … Ù A_n ® A) не может принимать значения 0, т.е. является законом логики, что и требовалось.

Пусть теперь (А₁ Ù … Ù A_n ® A) – закон логики. Рассмотрим любую интерпретацию e = (e₁ ; … ; e_k) со свойством A₁(e) = … = A_n(e) = 1. Тогда

1 = (А₁ Ù … Ù A_n ® A)(e) = (А₁(e) Ù … Ù A_n(e) ® A(e)) = (1 ® A(e)),

и по аксиоме вычисления импликации A(e) = 1. Таким образом, А₁ , … , A_n 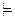A.

Теорема доказана.

Теорема (о дедукции).Для любого множества формул Г и формул А, B условие Г, А В выполнено тогда и только тогда, когда Г A ® B.

Доказательство. Условие Г, А В, где Г = {A₁ , … , A_n } (n ³ 0), имеет место (по доказанной выше теореме) в случае, когда (A₁ Ù …Ù A_n Ù A ® B) – закон логики.Имеем ((A₁ Ù …Ù A_n Ù A ® B) º 1)Û (( 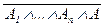Ú B) º 1)Û Û {де Морган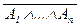} Û (( Ú 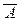Ú B) º 1)Û (( 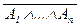Ú (A ® B)) º 1)Û Û ((A₁ Ù …Ù A_n ® (A ® B)) º 1). Таким образом, (A₁ Ù …Ù A_n Ù A ® B) – закон логики тогда и только тогда, когда законом логики является формула (A₁ Ù …Ù A_n ® (A ® B)),а это (по критерию логического следования) и означает, что Г, А В имеет место тогда и только тогда, когда Г A ® B.

Теорема доказана.

В течение тысячелетий человечеством накоплен опыт построения правильных выводов. Соответствующие правила на математическом языке обычно записывают так: 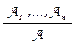, где А₁ , … , A_n – посылки, а А – заключение. Такое правило означает, что из справедливости посылок А₁ , … , A_n логически следует справедливость заключения А . На самом деле правила (логического) вывода представляют из зебя схемы правил: они зависят от переменных-параметров, вместо которых можно подставлять любые формулы исчисления высказываний. Эти параметры будем выделять курсивом.

Пример.Правило modus ponens – “мост ослов”: 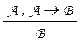[2] .

Здесь А , В – любые формулы языка исчисления высказываний. Докажем это правило. Для этого проверим, что А, А ® В В . Имеем (А, А ® В В ) Û Û (А ® В , А 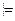В ) Û (А ® В А ® В ) Û (((А ® В ) ® (А ® В )) º 1), что справедливо.

Знак Û здесь, как обычно, следует понимать как синоним выражения “тогда и только тогда, когда”.

Теорема (об основных правилах логического вывода).Справедливы следующие основные правила логического вывода:

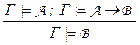– расширение modus ponens, 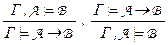– правила дедукции, 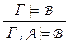– правило расширения посылок, 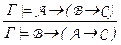–правило перестановки посылок, 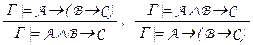– правила объединения и разделения посылок, 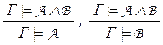– правила удаления конъюнкции, 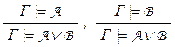– правила введения дизъюнкции, 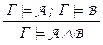– правило введения конъюнкции, 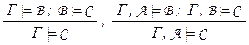– правила силлогизма, 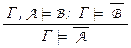– modus tollens [3], 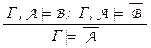– правило опровержения, 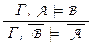– правило контрапозиции, 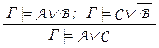– правило резолюций.

Доказательство. Правила расширение modus ponens доказывается аналогично его основному варианту. Правило дедукции уже доказано в теореме о дедукции. Остальные правила доказываются примерно так же.

Правило расширения посылок 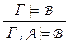. Действительно, условие Г B означает, что формула B принимает значение 1 на всех наборах значений переменных, при которых все формулы из Г имеют значения 1. Значит B принимает значение 1 и на всех наборах значений переменных, при которых имеют значения 1 формула A и все формулы из Г , т.е. Г, A B , что и требовалось доказать.

Правило перестановки посылок: 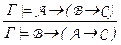. Дано Г 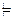A ® (B ® C ), т.е. (по теореме о дедукции) Г, A B ® C или Г, A , B 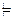C , что равносильно утверждению Г, B , A C . По теореме о дедукции, получим Г, B A ® C , и далее Г 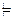B ® (A ® C ), что и требовалось.

Правило объединения и разделения посылок 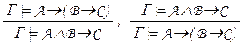. Можно рассудить иначе, чем раньше: нетрудно заметить, что A ® (B ® C ) º º (A Ù B) ® C . Поэтому если любая из этих формул истинна при любых значениях пропозициональных переменных, при которых истинны все формулы множества Г, то это же верно и для второй формулы. Таким способом можно доказать и предыдущее правило вывода.

Правила удаления конъюнкции 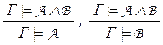. Если при любых значениях пропозициональных переменных, при которых истинны все формулы множества Г, истинна формула A Ù B, то это верно и для формул A и B .

Правила введения дизъюнкции 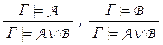и введения конъюнкции 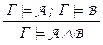докажите самостоятельно.

Правила силлогизма: 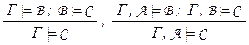. Первое из правил следует из того, что если Г B и (B ® C) – закон логики, то при любых наборах значений пропозициональных переменных, при которых истинны все формулы из множества Г, истинны B и B ® C , а значит и C , что и требовалось.

Второе правило можно вывести так: если Г , A B и Г , B C , то (по теореме о дедукции) Г A ® B и Г 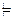B ® C , и по правилу введения конъюнкции верно Г 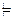(A ® B) Ù (B ® C). Закон логики (A ® B) Ù (B ® C )® (A ® C) позволяет по первому правилу силлогизма (?!) получить Г 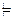A ® С , а значит, Г , A С по теореме о дедукции, что и требовалось.

Правило modus tollens 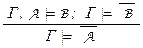. Действительно, из Г A ® B и Г 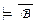по правилу введения конъюнкции следует Г (A ® B ) Ù 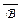. Учитывая закон логики (A ® B ) Ù 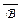® 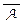, по первому правилу силлогизма получаем (?!) Г 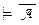, что и требовалось.

Правило опровержения 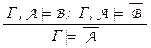можно вывести из Г 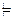A ® B , Г 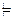A ® 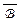и равносильности (A ® B ) Ù (A ® 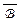) º 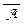(восстановите детали самостоятельно).

Правило контрапозиции 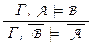следует из Г A ® B , теоремы одедукции и закона контрапозиции.

Правило резолюций 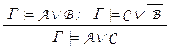: если оно не верно, то для некоторой интерпретации x₁ = e₁ , … , x_n = e_n , при которой все формулы из Г имеют значение 1, будет A(e) = 0 = C(e), что немедленно ведёт к противоречию: B(e) = (A(e) Ú B(e)) = 1 = (C(e) Ú 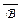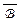(e)) = (e).

Теорема доказана.

Упражнение: Докажите все правила логического вывода при Г = Æ.