Определенный интеграл
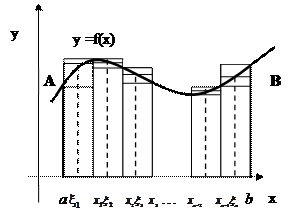 Геометрический смысл определенного интеграла
Геометрический смысл определенного интеграла
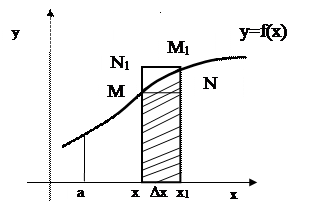
Задача. Оценить площадь криволинейной трапеции, ограниченной непрерывной кривой y=f(x) и прямыми y=0; x=a; x=b.
6 Рассмотрим криволинейную трапецию aABb . Ее площадь обозначим 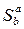
Интервал [a,b] разобьем на n частичных интервалов, не обязательно равных, точками деления: 
a< 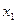 <
< 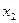 <...<
<...< 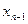 <b.
<b.
Каждый частичный интервал 
[ 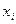 ,
, 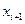 ] имеет длину, равную
] имеет длину, равную 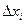 .
.
Внутри каждого интервала выберем точку 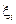 и вычислим f(
и вычислим f( 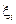 ).
).
Составим произведения:
f 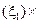
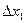 , f
, f 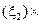
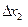 , ... , f
, ... , f 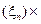
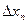 , которые представляют собой площади соответствующих прямоугольников.
, которые представляют собой площади соответствующих прямоугольников.
Очевидно, можно записать:
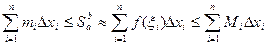 (1)
(1)
Где 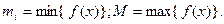
( 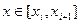 )
)
Сумма 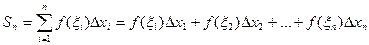 называется интегральной суммой функции f(x) на интервале [a, b].
называется интегральной суммой функции f(x) на интервале [a, b].
Если будем увеличивать число частичных интервалов, тем самым уменьшая их длину ( 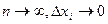 ), интуитивно ясно, что в неравенстве (1) левая, средняя и правая части неравенства в пределе будут стремиться к площади криволинейной трапеции.
), интуитивно ясно, что в неравенстве (1) левая, средняя и правая части неравенства в пределе будут стремиться к площади криволинейной трапеции.
Предел интегральной суммы функции f(x) на [a, b] при неограниченном уменьшении длины частичного интервала разбиения (соответственно, 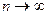 ), называется определенным интегралом функции f(x) на отрезке [a, b].
), называется определенным интегралом функции f(x) на отрезке [a, b].
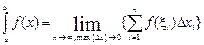
Определенный интеграл соответствует площади криволинейной трапеции.
 Формула Ньютона – Лейбницаустанавливает связь между понятиями неопределенного и определенного интеграла.
Формула Ньютона – Лейбницаустанавливает связь между понятиями неопределенного и определенного интеграла.
ТЕОРЕМА. Функция Ф(x), выражающая площадь переменной криволинейной трапеции (с подвижной правой стороной) является первообразной для функции y=f(x), графиком которой является кривая, ограничивающая эту трапецию сверху.
6 Имеет место неравенство:
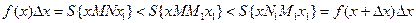
площадь площадь площадь
4-угольника крив.трапеции 4-угольника
Если обозначим 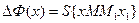 , то отсюда:
, то отсюда: 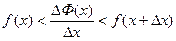
Если 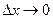 , то в силу непрерывности f(x):
, то в силу непрерывности f(x):
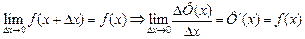
Этим доказано, что функция Ф(x), выражающая площадь криволинейной трапеции, является первообразной для f(x).
Можно записать: 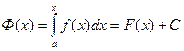
(F(x) – некоторая первообразная для f(x)).
Определим константу С:
- при x=a, Ф(a)=F(a)+C=0ÞC= –F(a), т.е.
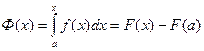
- при x=b, получим:
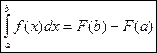 - формула Ньютона – Лейбница.
- формула Ньютона – Лейбница.
Пример: Вычислить 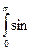 xdx
xdx
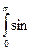 xdx =
xdx = 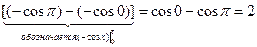
Дата добавления: 2016-06-05; просмотров: 1414;











