Приложения определенного интеграла


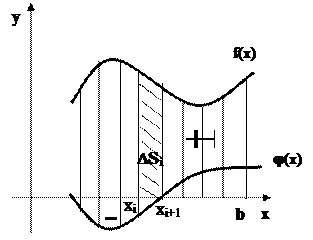I. Площадь плоской фигуры

Задача: Найти площадь криволинейной

трапеции, ограниченной линиями:

y=f(x), y= 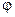(x), x=a, x=b

В качестве элемента интегральной

суммы 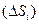примем:

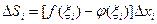, где

;

 

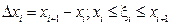Пример Найти площадь фигуры, ограниченной линиями: y= .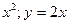

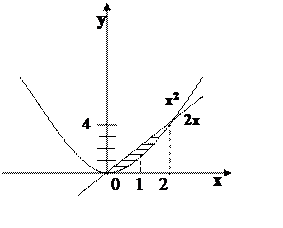
Точка пересечения: .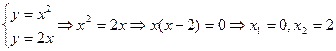

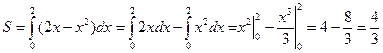
II. Объем тела вращения

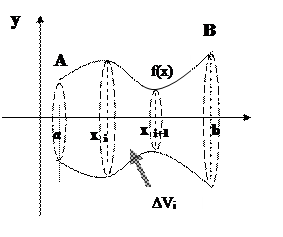
Найти объем тела (V), образованного вращением вокруг оси Ох криволинейной трапеции aABb ={x=a; x=b; y=0; y=f(x)}.

 

6 элемент интегральной суммы –

объем диска.

 

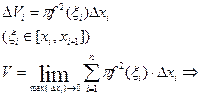
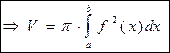
Пример: Определить объем тела, ограниченного поверхностью, полученной от вращения эллипса вокруг оси Ox.

6 Уравнение эллипса:

x

 

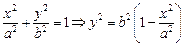
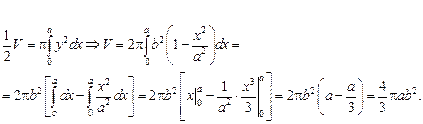
В частности, объем шара при a=b=r:

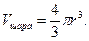
Задачи для самостоятельного решения

1. Оценить объем бочки, высотой h=1 м, длина обруча в основании 0,8p, центрального обруча –p.

Указание: Принять приближенно, что боковая поверхность бочки образована вращением параболы вокруг оси Ох.

2. Высота кучи зерна, имеющего коническую форму, равна 2,5 м, а окружность ее основания 20 м. Масса 1 м3 зерна равна 750 кг. Какова масса зерна в куче?

(Применить формулу объема тела вращения).


Дата добавления: 2016-06-05; просмотров: 1290;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, тогда расскажите друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2024 год. Материал предоставляется для ознакомительных и учебных целей.
Генерация страницы за: 0.008 сек.