Исследование функций
График функции y = f(x) называется выпуклым (вогнутым) в области D 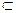 R, если соответствующий отрезок кривой y = f(x) расположен ниже (соответственно выше) касательной в каждой точке области D.
R, если соответствующий отрезок кривой y = f(x) расположен ниже (соответственно выше) касательной в каждой точке области D.

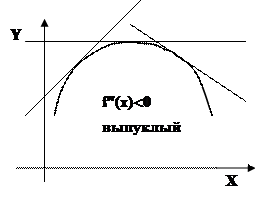

Мнемоническое правило:
Знак 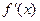 “+” – вода из “чашки” не выливается – функция вогнута,
“+” – вода из “чашки” не выливается – функция вогнута,
Знак 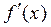 “-” – вода из “чашки” выливается – функция выпукла.
“-” – вода из “чашки” выливается – функция выпукла.
Примем без доказательства.
Точка на графике кривой 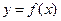 ,при переходе через которую кривая из выпуклой становится вогнутой (или наоборот) называется точкой перегиба кривой.
,при переходе через которую кривая из выпуклой становится вогнутой (или наоборот) называется точкой перегиба кривой.
Очевидно, что точки перегиба, это точки на кривой, где 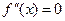
Асимптота – это прямая, лучом которой в окрестности бесконечно удаленной точки можно приближенно заменить соответствующий участок кривой.
Если прямая 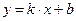 - асимптота кривой
- асимптота кривой 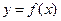 при
при
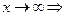
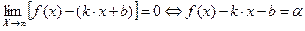 (бесконечно малая)
(бесконечно малая)
Деля на x:
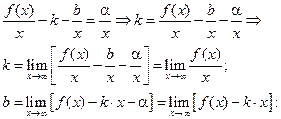
Пример: Исследовать функцию 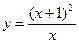 и построить ее график.
и построить ее график.
Область определения: 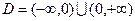 функция непрерывна в области определения.
функция непрерывна в области определения.
Поведение на границах области:
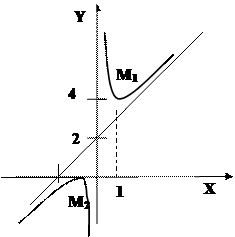
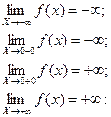
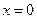 - вертикальная асимптота.
- вертикальная асимптота.
Пересечение с осями:
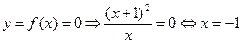
Экстремумы функции:
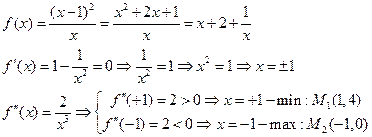
Точки перегиба: 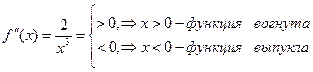
Асимптоты:
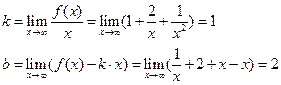
Асимптота: 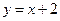
Теорема Ролля : Если функция f(x) непрерывна на 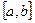 , дифференцируема на (a, b) и
, дифференцируема на (a, b) и 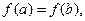 то существует хотя бы одна точка
то существует хотя бы одна точка 
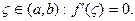
6 Если 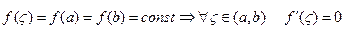
Если 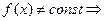 найдется хотя бы одна точка
найдется хотя бы одна точка 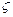
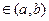 ,в которой достигается локальный экстремум.
,в которой достигается локальный экстремум.
Очевидно, 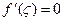 .
.
Теорема Коши: Если функции f(x) и 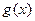 : непрерывны на отрезке
: непрерывны на отрезке 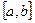 , дифференцируемы на интервале (a, b),
, дифференцируемы на интервале (a, b), 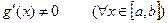 , тогда найдется такая точка
, тогда найдется такая точка 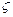
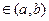 в которой выполняется
в которой выполняется
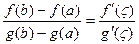
|
6 Введем вспомогательную функцию
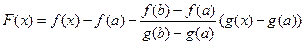
Не трудно убедиться, что она удовлетворяет всем условиям теоремы Ролля.
Значит найдется 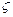
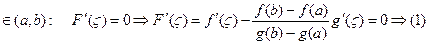
Теорема Лагранжа: Если функция f(x) непрерывна на отрезке 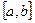 , дифференцируема на интервале(a, b), тогда найдется такая точка
, дифференцируема на интервале(a, b), тогда найдется такая точка 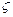
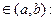
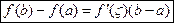 (2)
(2)
6 Эта теорема – частный случай теоремы Коши, если взять 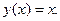
Так как 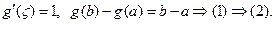
Задача: С помощью формулы Лагранжа (2) найти приближенное значение 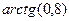
6 Возьмем 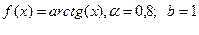 . Условия теоремы Лагранжа выполняются, значит существует
. Условия теоремы Лагранжа выполняются, значит существует 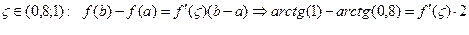
Так как 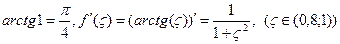
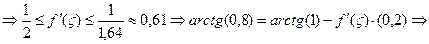
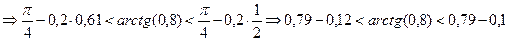
Þ 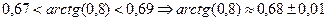
Дата добавления: 2016-06-05; просмотров: 1289;











