Интегрирование по частям

Пусть u(x), v(x) – дифференцируемые функции, тогда: d(uv)=udv+vduÞudv=d(uv)-vdu.

Интегрируя обе части:

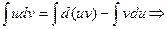
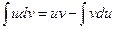
Пример:

9) Вычислить

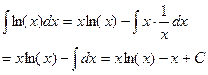
Вспомогательные вычисления: u=ln (x) du=dx/x dv=dx ; v=x

Пример 10

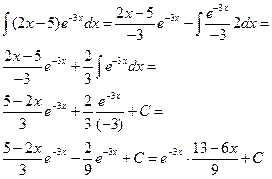
u=2x-5 du=2dx dv= 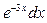v=

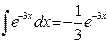
Задача: Скорость движения тела задана уравнением V=4t²+1 (м/сек).

Найти уравнение движения, если к моменту t=3сек. пройден путь S=60м.

6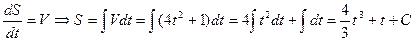

Константа С определяется из условия: S(3)= 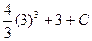=60ÞC=60-3-36=21(м)

Окончательно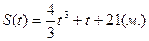

Задачи для самостоятельного решения:

1. Скорость прироста популяции бактерий описывается функцией 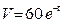(ос./час)

Если начальная численность популяции составляла 40 особей, то

а) Какова предельная численность популяции?

б) Через какое время численность популяции удвоится?

2. Касательная, проведенная к графику функции y=f(x) имеет угловой коэффициент, величина которого обратна квадрату абсциссы точки касания. Найти уравнение линии если известно, что она проходит через точку А(1,3).

Контрольные вопросы

1) Дайте определение первообразной функции

2) Сформулируйте основные свойства неопределенного интеграла.

3) Назовите основные методы интегрирования. В чем их суть?