Приложения производной

Задачи с практическим содержанием на отыскание экстремума функции.

Задача 1: Масса животного, например быка (при правильных условиях содержания) – известная функция времени, т.е. возрастает по определенному закону: 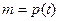(кг).

Затраты на откорм одной головы можно приближенно описать линейной функцией времени: 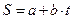, где

a – цена молодняка приобретенного хозяйством;

b – затраты на содержание 1 головы в единицу времени.

Определить оптимальный срок откорма.

6 Обозначим 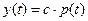- стоимость произведенного продукта (c – const; стоимость 1 кг мяса).

Функция прибыли выразится:

П 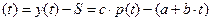, где

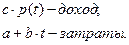
Для нахождения максимума функции П(t):

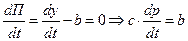
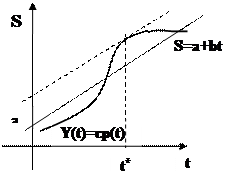
Вывод: Максимуму прибыли соответствует такое значение момента времени t*, для которого угловой коэффициент касательной к графику функции стоимости продукта, равен угловому коэффициенту прямой – графика функции затрат.

Т.е. при t= t* касательная к графику функции y(t) параллельна прямой затрат

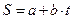
Задача 2: В питательную среду вносят популяцию из 1000 бактерий. Численность популяции возрастает согласно уравнению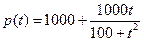

(t – время в часах).

Найти максимальный размер популяции.

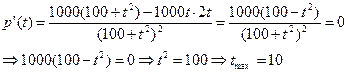
Проверка: 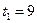час < 10 час,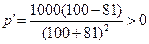

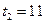час > 10 час,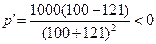

Вывод: максимальный размер популяции составляет

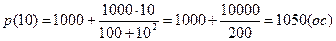
достигается по прошествии 10 часов роста.