Первообразная. Правила интегрирования
Если при определении дифференциала функции, по заданной функции y=f(x) отыскивали ее производную 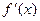 , то при интегрировании имеем дело с обратной задачей: по заданной производной отыскать исходную функцию (первообразную).
, то при интегрировании имеем дело с обратной задачей: по заданной производной отыскать исходную функцию (первообразную).
Функция F(x) называется первообразной по отношению к функции f(x), если для каждого xÎ(a,b) 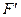 (x)=f(x) и dF(x)=f(x)dx.
(x)=f(x) и dF(x)=f(x)dx.
Примеры:
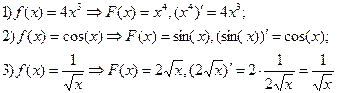
Если отыскание производной операция однозначная, то отыскание первообразной данной функции – операция неоднозначная.
Если F(x) – первообразная f(x), то F(x)+C (C - const) – также первообразная функции f(x).
6 По условию 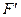 (x) = f(x), тогда (F(x)+C
(x) = f(x), тогда (F(x)+C 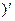 =
= 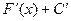 =f(x).
=f(x).
Операция отыскания первообразной для данной непрерывной функции функции называется интегрированием а вся совокупность первообразных называется неопределенным интегралом этой функции.
Записывается:
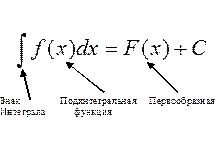
Свойства неопределенного интеграла
Пусть f(x), g(x) – непрерывные функции , k=const.
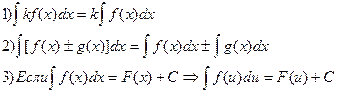
Вид интеграла не изменится при переходе от переменной x к переменной u, где u=u(x) – дифференцируемая функция от x.
Таблица неопределенных интегралов
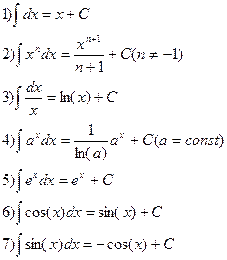
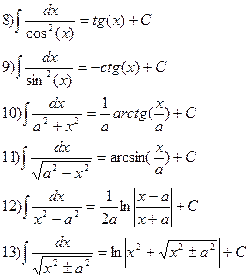
Задача интегрирования сводится, в простейшем случае, к элементарным преобразованиям, приводящим подинтегральную функцию к виду какого либо табличного интеграла.
Примеры. Найти первообразную:
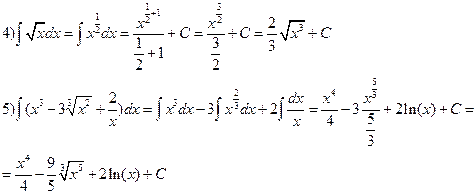
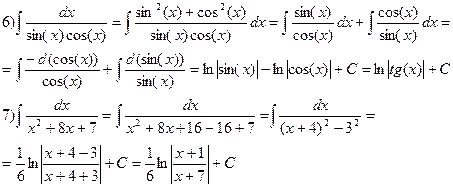
Дата добавления: 2016-06-05; просмотров: 2593;











