Механический смысл производной
Пусть при неравномерном прямолинейном движении величина пути, пройденного телом: 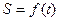 (t-время)
(t-время)
Пусть 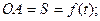
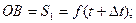
Тогда 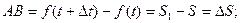
Средняя скорость на отрезке 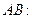
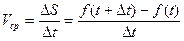
Мгновенная скорость в точке 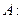
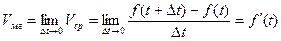
Мгновенная скорость при неравномерном прямолинейном движении точки характеризует механический смысл производной (от функции пути).
Примеры:
1) Найти значение мгновенной скорости свободно падающего (в пустоте) тела через 3 сек. падения.
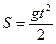 (
( 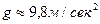 )
)
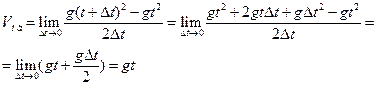
Если 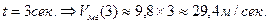
2) Для функции 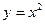 найти значение углового коэффициента касательной при x=1.
найти значение углового коэффициента касательной при x=1.
|
|
|

K = 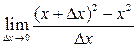 =
= 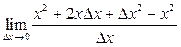
= 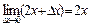
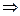
K(1) = 2´1 = 2 = tg(b)Þb= arctg2 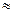 630.
630.
3) Некоторая популяция микроорганизмов в момент времени t насчитывает 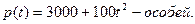
Оценить мгновенную скорость роста популяции через 5 часов развития.
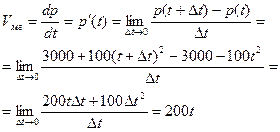

При 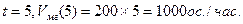
Таблица производных основных элементарных функций
| № | 
| 
| |
| C | c, a – const | ||
| u(x), v(x) дифференцируемые функции | ||
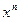
| 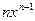
| ||
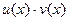
| 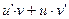
| ||
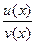
| 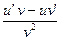
| ||
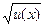
| 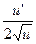
| ||
| ex | ex | ||
| ax | 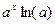
| ||
| ln(x) | 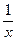
| ||
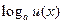
| 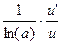
| ||
| Сu(x) | С 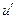
| ||
| sin(x) | cos(x) | ||
| cos(x) | - sin(x) | ||
| tg(x) | 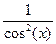
| ||
| ctg(x) | 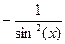
| ||
| arcsin(x) | 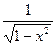
| ||
| arcos(x) | 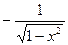
| ||
| arctg(x) | 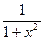
| ||
| arcctg(x) | 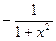
| ||
| u(v(x)) | 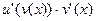
|
Пример. Найти производную функции 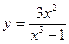 и вычислить
и вычислить 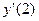 .
.
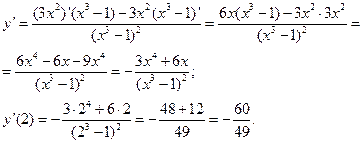
Дата добавления: 2016-06-05; просмотров: 1570;











