Понятия: непрерывная функция, точки разрыва функции.

Примеры некоторых непрерывных функций:

у=Т(t) – температура воды ( 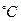) в зависимости от времени нагревания;

у=Р(t) – вес животного (кг) в зависимости от времени откорма (t);

y=S(t) – путь, пройденный автомобилем в зависимости от времени.

Пусть задана функция аргумента x: y=f(x).

Обозначим:

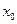- исходное значение аргумента;

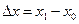- приращение аргумента;

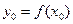- исходное значение функции;

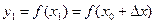- наращенное значение функции;

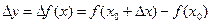- приращение функции в точке x₀;

Функция y=f(x) называется непрерывной в точке x₀, если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции.

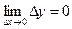
Функция y=f(x) – непрерывна на числовом интервале 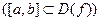, если она непрерывна в любой точке этого интервала.

Пример: Урожайность зерна кукурузы f(x) (ц/га) в зависимости от количества внесенного в почву азотного удобрения (х, кг) выражается формулой .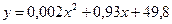

Является ли данная функция непрерывной?

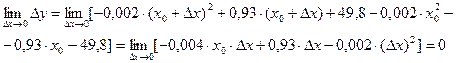
Здесь пользуемся свойством пределов функций, что если 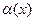- бесконечно малая, а g(x) – ограниченная 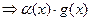- бесконечно малая. Функция y=f(x) – непрерывна на всей числовой оси.

Задача: Функция y=f(x) определена и непрерывна в точке x₀.

Найти предел функции в этой точке.

6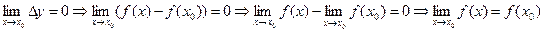

Функция f(x) непрерывна в точке x₀, если предел функции в этой точке равен значению функции в этой точке.

Пример: Показать непрерывность функции 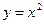в точке x₀=2.

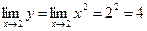
Односторонние пределы

Число А называется пределом функции f(x) в точке x₀ справа (слева), если для любого 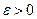, найдется 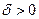, что при 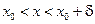( 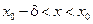) выполняется 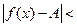e и записывают:

Правосторонний предел: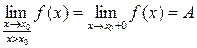

Левосторонний предел: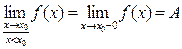

Функция f(x) непрерывна при 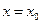, если выполняются следующие условия:

1) Функция y=f(x) определена не только в точке x₀, но и в некотором интервале, содержащем x₀;

2) Функция y=f(x) при 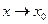имеет конечные и равные между собой односторонние пределы;

3) Односторонние пределы при 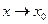совпадают со значением функции в точке x₀, т.е.

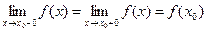
Если для данной функции f(x) хотя бы одно из перечисленных условий не выполняется, то функция называется разрывной в точке .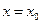

Функция f(x) имеет в точке x₀ разрыв 1 рода, если односторонние пределы слева и справа существуют, но не равны между собой (или, может быть, существуют и равны между собой но не равны значению f( x₀)).

Если хотя бы один из односторонних пределов не существует (или равен бесконечности), то разрыв в этой точке называется разрывом 11 рода.

Пример: Исследовать на непрерывность функции:

1)

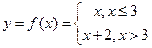
Левосторонний предел в точке х=3:

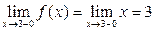
Правосторонний предел:

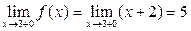
В точке х=3 функция f(x) имеет разрыв 1 рода.

Скачок функции (в точке х=3).

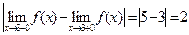
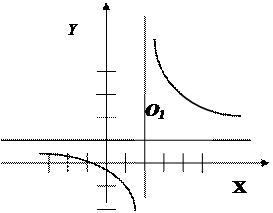
2)

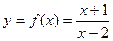
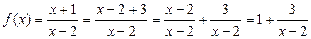
Функция не определена при х=2.

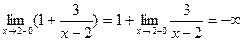
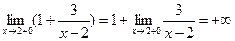
Точка х=2 – точка разрыва II рода.

График – две ветви гиперболы с центром

симметрии в точке 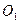(2,1).