Волновая функция и ее статистический смысл

Положение частицы в пространстве в данный момент времени в квантовой механике определяется знанием волновой функции Ψ. Вероятность dw того, что частица находится в элементе объема dV, пропорциональна квадрату модуля волновой функции |Ψ|² и объему элемента dV

dw = |Ψ|² dV

Величина |Ψ|² = 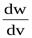(квадрат модуля Ψ-функции) имеет смысл плотности вероятности, т.е. определяет вероятность нахождения частицы в единичном объеме в окрестности точки с координатами x, y, z.

Таким образом, физический смысл имеет не сама Ψ-функция, а квадрат ее модуля |Ψ|². Вероятность найти частицу в момент времени t в конечном объеме V согласно теореме сложения вероятностей, равна

.

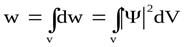Волновую функцию необходимо нормировать таким образом, чтобы вероятность достоверного события обращалась в единицу. Это будет выполняться, если за объем интегрирования V принять бесконечный объем всего пространства. Условия нормировки вероятностей:

,

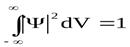где интеграл вычисляется по всему бесконечному пространству, т.е. по координатам x, y, z от -∞ до +∞.

При этом волновая функция должна удовлетворять трем раннее перечисленным условиям:

1. Должна быть конечной (вероятность не может быть больше 1).

2. Должна быть однозначной (вероятность не может быть неоднозначной величиной).

3. Должна быть непрерывной (вероятность не может изменяться скачком).

Потенциальная яма – ограниченная область пространства с пониженной потенциальной энергией частицы. Потенциальная яма обычно отвечает короткодействующим силам притяжения. В области действия этих сил потенциал отрицателен, вне – нулевой.

Итак, пусть частица массы m находится в одномерной потенциальной яме бесконечной глубины (рис. 2). Потенциальная энергия U удовлетворяет следующим граничным условиям

.

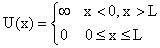(1

При таких граничных условиях частица находится внутри потенциальной ямы 0 < x < L и не может выйти за ее пределы, т.е.

Используя станционарное уравнение Шредингера для случая U = 0, получим

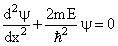
(3)

Уравнение (3) описывает положение частицы внутри потенциальной ямы.
Для бесконечной одномерной потенциальной ямы имеем следующее:

1. Энергия частицы принимает определенные дискретные значения. Обычно говорят, что частица находится в определенных энергетических состояниях. 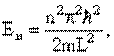где n = 1, 2, 3...

2. Частица может находиться в каком-то одном из множества энергетических состояний.

3. Частица не может иметь энергию равную нулю.

4. Каждому значению энергии E_n соответствует собственная волновая функция ψ_n, описывающая данное состояние.

5. Для собственной функции ψ₁(x) вероятность обнаружить частицу в точке x = L/2 максимальна. Для состояния ψ₂(x) вероятность обнаружения частицы в этой точке равна 0 и так далее.

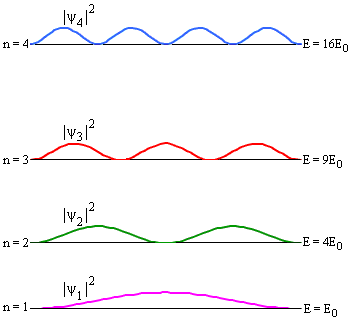Рис. 2. Плотности вероятности обнаружения частицы в различных квантовых состояниях.

Потенциальный барьер – область пространства, где потенциальная энергия частицы (или тела) выше, чем в соседних областях. Рассмотрим простейший потенциальный барьер прямоугольной формы шириной а и высотой U₀. Вне барьера потенциальная энергия частицы равна нулю. Полная энергия частицы Е равна сумме её кинетической энергии Т и потенциальной U. Вне барьера Е = Т. Если частица двигается на барьер слева и имеет Е = Т < U₀, то с точки зрения классической физики она не может преодолеть его и отразится от него. Действительно, классическая физика требует безусловного сохранения энергии. Если представить, что частица с Е < U₀, вошла внутрь барьера, то она неизбежно должна иметь там отрицательную кинетическую энергию (чтобы её полная энергия сохранилась), что невозможно по смыслу кинетической энергии.
С точки зрения квантовой физики частица с Е < U₀ может с некоторой вероятностью пройти сквозь барьер. Это явление носит название туннельного эффекта.
Вероятность прохождения частицы массы m через барьер D определяется соотношением

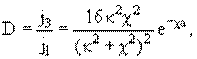
где .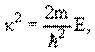
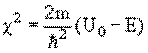Основная зависимость коэффициента прохождения D от ширины a и высоты барьера U₀ определяется экспоненциальным множителем e^-χa.

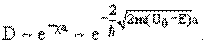
В случае a ~ 10^-13 см, m ~ 10^-24 г для (U₀ − E) ~ 10 МэВ D ~ 1/e.
То есть частица (протон, α-частица) с заметной вероятностью может пройти сквозь потенциальный барьер, превышающий её энергию на 5–10 МэВ.