Понятие дифференциала функции

В соответствии с определением производной и предела:

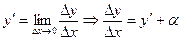( a– бесконечно малое при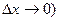

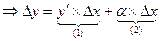
При 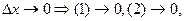но

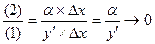
То есть порядок малости (2) выше, чем порядок малости (1) при .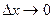

Выражение 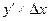- главная часть приращения 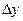- называется дифференциалом функции 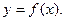Обозначается .

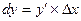Так как при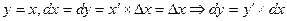

Дифференциал функции равен произведению её производной на дифференциал (или приращение) независимой переменной.

Применение дифференциала
(для приближенного вычисления приращения функции)

Задача 1 Оценить, на сколько увеличится объем металлического куба со стороной 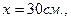если при нагревании каждая сторона его увеличилась на 1мм. (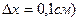

6Имеем функцию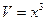

Так как 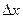мало по сравнению с x, то можно считать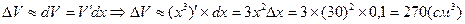

Точное значение: =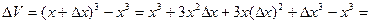

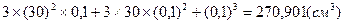
Погрешность вычисления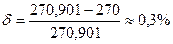

Экстремум функции

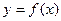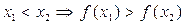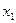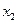
Функция , называется убывающей на интервале (a, b), если для всех точек этого интервала при . Если же из < 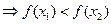, то функция возрастающая.

Теорема: Если дифференцируемая в промежутке (a; b) функция y = f(x) имеет в каждой точке 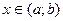положительную (или отрицательную) производную, то эта функция возрастает (или убывает) на данном промежутке.

6 По определению производной:

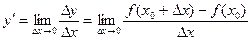
Из 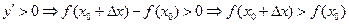- функция убывает.

Функция y = f(x) имеет максимум ( минимум) при 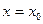, если 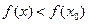(соответственно 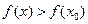) для всех 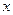, достаточно близких 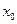( 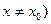.Точки минимума и максимума называются точками экстремум.