Волновая функция и ее статистический смысл
В общем случае (произвольное движение частицы в произвольных силовых полях) состояние частицы в квантовой механике задается волновой функцией (или пси -функцией) 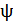 зависящей от координат и времени:
зависящей от координат и времени: 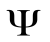 (x, y, z ,t). Она – основной носитель информации о корпускулярных и волновых свойствах микрочастиц. В частном случае свободного движения частицы волновая функция – плоская волна де Бройля.
(x, y, z ,t). Она – основной носитель информации о корпускулярных и волновых свойствах микрочастиц. В частном случае свободного движения частицы волновая функция – плоская волна де Бройля.
Статистическая интерпретация волновой функции
На основании статистической интерпретации вероятность нахождения частицы в момент времени t с координатами х и х+dx, y и y+dy, z и z+dz, определяется интенсивностью волновой функции, т.е. квадратом пси - функции. Поскольку в общем случае пси – функция – комплексная функция, а вероятность должна быть всегда действительной и положительной величиной, то за меру интенсивности принимается квадрат модуля волновой функции. Для одномерного движения (например, в направлении оси Ox ):
| 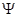 (x,t)|2=
(x,t)|2= 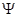 (x,t)
(x,t) 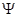 *(x,t) или
*(x,t) или 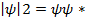 , где
, где
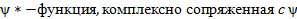
Физический смысл пси – функции: Вероятность dW нахождения частицы в элементе объема dV в момент времени t:
dW=| 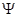 |2dV
|2dV
Плотность вероятности, т.е. вероятность нахождения частицы в момент времени t в окрестности данной точки пространства:
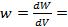 |
| 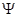 |2
|2
Плотность вероятности - величина, наблюдаемая на опыте, в то время как сама волновая функция, являясь комплексной, наблюдению недоступна. В этом заключается существенное отличие в описании состояний частиц в квантовой и классической механике (в классической механике величины, описывающие состояние частиц, наблюдаемы.)
Вероятность найти частицу в момент времени t в некотором объеме V.
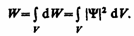
Условие нормировки вероятности: 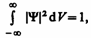
Так как 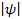 2 dV определяется как вероятность, то проинтегрировав это выражение в бесконечных пределах, получим вероятность того, что частица в момент времени t находится где - то в пространстве. Это есть вероятность достоверность события, а ее в теории вероятности считают равной 1.
2 dV определяется как вероятность, то проинтегрировав это выражение в бесконечных пределах, получим вероятность того, что частица в момент времени t находится где - то в пространстве. Это есть вероятность достоверность события, а ее в теории вероятности считают равной 1.
Волновая функция – объективная характеристика состояния микрочастиц и должна удовлетворять ряду ограничений. Она должна быть конечной (вероятность не может быть больше 1), однозначной (вероятность не может быть неоднозначной величиной) и непрерывной (вероятность не может изменяться скачком).
Принцип суперпозиции состояний для волновых функций
Если какая либо система (частица или совокупность) может находится в различных состояниях, описывающих волновыми функциями  то она может находиться в состоянии
то она может находиться в состоянии 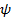 , описываемой линейной комбинацией этих функций.
, описываемой линейной комбинацией этих функций.
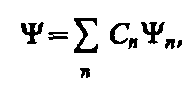
Сn (n=1.2,…) – произвольные (в общем случае комплексные) числа, при этом квадрат модуля коэффициента Сn, т.е. 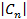 2, равен вероятности обнаружить, что система, представленная состоянием
2, равен вероятности обнаружить, что система, представленная состоянием 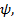 может оказаться в состоянии
может оказаться в состоянии 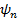 .
.
Дата добавления: 2017-11-21; просмотров: 3387;











