Задачи для самостоятельного решения

1. Дана функция y= 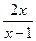и два значения аргумента x₁=1, x₂=2.

А) Проверьте, является ли данная функция непрерывной или разрывной при данных значениях аргумента.

Б) Найдите односторонние пределы в точках разрыва.

В) Постройте график функции на интервале [-6, 6].

2. Вещественная функция f(x) задается как:

f(x) =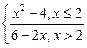

Найдите односторонние пределы и скачок функции в точке разрыва.

Постройте график функции на интервале [-4, 4].

Контрольные вопросы

1) Определение непрерывности функции в точке.

2) Определение левостороннего, правостороннего предела функции в точке.

3) Связь понятия непрерывности и наличия односторонних пределов функции в точке.

4) Определение разрыва I и II рода функции в точке.

5) Основные теоремы о непрерывных функциях.

Понятие производной и дифференциала функции

Производной функции f(x) в точке x₀ называется предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю.

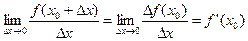
В соответствии с определением предела:

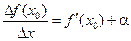, где a - бесконечно малое при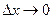

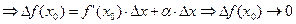
(при 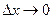) 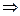функция f(x) непрерывна в точке x₀.