Волновая функция и ее статистический смысл

Мы привыкли к тому, что физически реальное – измеримо. Бор и Гейзенберг сделали обратное высказывание: «Принципиально неизмеримое – физически нереально». Поэтому «не надо говорить о вещах, которые невозможно измерить» (Фейнман). Поскольку из соотношения неопределенностей следует, что частица не имеет одновременно импульс и координату, то не следует об этом и говорить. А «говорить» следует о волновой функции, которая описывает микросостояние системы, ее волновые свойства.

Де Бройль связал со свободно движущейся частицей плоскую волну. Известно [cм. (1.5), (1.6)], что плоская волна, распространяющаяся в направлении оси х описывается уравнением

S=Acos(wt- kх+j_О)

или в экспоненциальной форме

S=А_Oехр[i(wt- kх+j_О)].

Заменив в соответствии с (1) и (2) w и k=2p/l через Е и p, уравнение волны де Бройля для свободной частицы пишут в виде

Y=А_Oехр[(-i/ 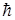)(Еt- pх)] (16)

(в квантовой механике показатель экспоненты берут со знаком минус, но поскольку физический смысл имеет çY÷ ², то это [cм. (16)] несущественно).

Функцию Y называют волновой функций или пси-функцией. Она, как правило, бывает комплексной.

Интерпретацию волновой функции дал в 1926 г. Борн: квадрат модуля волновой функции определяет вероятность того, что частица будет обнаружена в пределах объема dV:

dP=çY÷ ² dV=YY^*, (17)

где Y^* –комплексно-сопряженная волновая функция.

Величина çY÷ ²=YY^* = dP/ dV – имеет смысл плотности вероятности.

Интеграл от (17), взятый по всему пространству, должен равняться единице (вероятность достоверного события Р=1).

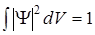(18)

Выражение (18) называют условием нормировки.

Отметим еще раз, что волновая функция описывает микросостояние частицы, ее волновые свойства, и она позволяет ответить на все вопросы, которые имеет смысл ставить. Например, найти энергию и импульс частицы. Для этого следует вычислить следующие частные производные Y по координате х и времени t:

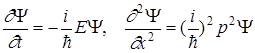
откуда

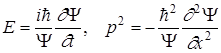. (19)